Câu 29 trang 117 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.
Đề bài
Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.
Lời giải chi tiết
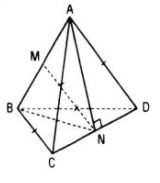
Gọi M, N lần lượt là trung điểm của AB và CD
ΔACD cân nên AN ⊥ CD và ΔBCD cân nên BN ⊥ CD.
Do đó CD ⊥ (ABN) suy ra CD ⊥ MN.
Tương tự ta cũng có AB ⊥ MN
Vậy d(AB, CD) = MN
Ta có:
\(\eqalign{ & M{N^2} = A{N^2} - A{M^2} = A{D^2} - N{D^2} - A{M^2} \cr & = {a^2} - {{c{'^2}} \over 4} - {{{c^2}} \over 4} = {1 \over 4}\left( {4{a^2} - c{'^2} - {c^2}} \right) \cr} \)
Vậy \(MN = {1 \over 2}\sqrt {4{a^2} - c{'^2} - {c^2}} \) với điều kiện \(4{a^2} > {c^2} + c{'^2}\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 29 trang 117 SGK Hình học 11 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 29 trang 117 SGK Hình học 11 Nâng cao timdapan.com"







