Câu 10 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K theo thứ tự là hai điểm trong của các tam giác ABC và BCD. Giả sử đường thẳng IK cắt mặt phẳng (ACD) tại J. Hãy xác định giao điểm J đó.
Đề bài
Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K theo thứ tự là hai điểm trong của các tam giác ABC và BCD. Giả sử đường thẳng IK cắt mặt phẳng (ACD) tại J. Hãy xác định giao điểm J đó.
Lời giải chi tiết
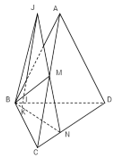
Ta chọn một mặt phẳng chứa IK và tìm giao tuyến của mặt phẳng này với mp(ACD) thì giao điểm của giao tuyến đó với IK chính là điểm J cần tìm.
Xét mp(BJK), gọi M, N lần lượt là các giao điểm của các cặp đường thẳng BI với CA và BK với CD. Khi đó:
\(\left( {BIK} \right) \cap \left( {ACD} \right) = MN.\)
Từ đó J chính là giao điểm của đường thẳng MN với đường thẳng KI.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 10 trang 51 Sách bài tập Hình học 11 nâng cao. timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 10 trang 51 Sách bài tập Hình học 11 nâng cao. timdapan.com"







