Bài tập 1 trang 126 Tài liệu dạy – học Toán 8 tập 2 - Hình học
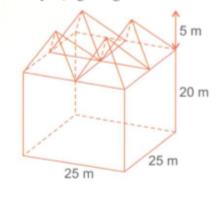
Giải bài tập Người ta muốn làm một cái nhà kho bằng tôn hình lăng trụ tứ giác đều có mái che là bốn hình chóp tứ giác đều với kích thước đã cho trên hình.
Đề bài
Người ta muốn làm một cái nhà kho bằng tôn hình lăng trụ tứ giác đều có mái che là bốn hình chóp tứ giác đều với kích thước đã cho trên hình.
a) Tính diện tích tôn cần thiết dùng để lợp mái và che xung quanh.
b) Tính thể tích không khí trong kho sau khi xây dựng xong.
Lời giải chi tiết
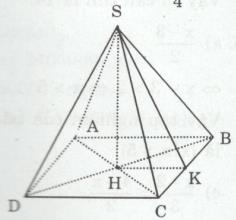
a) Diện tích tồn cần thiết dùng để lớp mái và che xung quanh chính là diện tích xung quanh của bốn hình chóp tứ giác đều và diện tích xung quanh của hình hộp chữ nhật.
Hình chóp tứ giác đều có độ dài cạnh đáy là 25 : 2 = 12,5 (m)
H, M lần lượt là trung điểm của AC và BC
=> HM là đường trung bình của ∆ABC \( \Rightarrow HM = {{AB} \over 2} = {{12,5} \over 2} = 6,25(m)\)
Trung đoạn của hình chóp đều là: \(d = SM = \sqrt {S{H^2} + H{M^2}} \)\(\, = \sqrt {{5^2} + 6,{{25}^2}} = {{5\sqrt {41} } \over 4}(m)\)
Diện tích xung quanh của một hình chóp đều là:
\({S_{xq1}} = p.h = 2.12,5.{{5\sqrt {41} } \over 4} = {{125\sqrt {41} } \over 4}({m^2})\)
Diện tích xung quanh của hình hộp chữ nhật là:
\({S_{xq2}} = 2ph = 4.25.20 = 2000({m^2})\)
Diện tích tôn cần dùng là:
\({S_{xq}} = 4.{S_{xq1}} + {S_{xq2}} = 125\sqrt {41} + 2000 \)\(\,\approx 2800,4({m^2})\)
b) Thể tích của một hình chóp đều:
\({V_1} = {1 \over 3}.{S_{ABCD}}.SH = {1 \over 3}.12,{5^2}.5\)\(\, = {{3125} \over {12}}({m^3})\)
Thể tích của hình hộp chữ nhật:
\({V_2} = a.b.c = 25.25.20 = 12500({m^3})\)
Thể tích không khí trong kho sau khi xây dựng xong:
\(V = 4.{V_1} + {V_2} = {{3125} \over 3} + 12500\)\(\, \approx 13541,67({m^3})\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 1 trang 126 Tài liệu dạy – học Toán 8 tập 2 - Hình học timdapan.com"