Bài 9 trang 92 SGK Toán 7 tập 2

Đề bài

Chứng minh rằng: Nếu tam giác \(ABC\) có đường trung tuyến xuất phát từ \(A\) bằng một nửa cạnh \(BC\) thì tam giác đó vuông tại \(A.\)

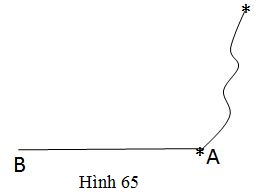
Ứng dụng: Một tờ giấy bị rách ở mép (h.65). Hãy dùng thước và compa dựng đường vuông góc ở cạnh \(AB\) tại \(A.\)

Lời giải chi tiết

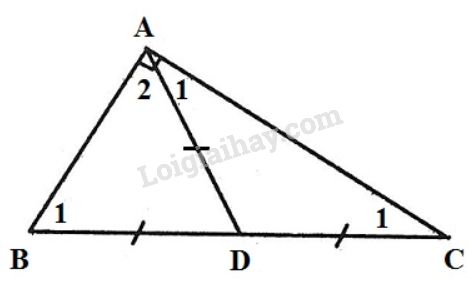
Giả sử \(∆ABC\) có \(AD\) là đường trung tuyến ứng với \(BC\) và  \(AD = \dfrac{1}{2}BC\).  

\( \Rightarrow   AD = BD = DC\). 

Hay \(∆ADC, ∆ADB\) cùng cân tại \(D\). Do đó: 

 \(\left. {\matrix{ {\widehat {{A_1}} = \widehat {{C_1}}}  \cr  {\widehat {{A_2}} = \widehat {{B_1}}}  \cr  } } \right\} \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} = \widehat {{B_1}} + \widehat {{C_1}}\)

Mà  \(\widehat {{A_1}} + \widehat {{A_2}} + \widehat {{B_1}} + \widehat {{C_1}}\)\(=\widehat {{BAC}}+ \widehat {{B_1}} + \widehat {{C_1}} = {180^o}\) (Theo định lí tổng ba góc trong \(∆ABC\))

\( \Rightarrow \)  \(\widehat {{A_1}} + \widehat {{A_2}} = \dfrac{180^0}{2}={90^o}\)

Hay \(∆ABC\) vuông tại \(A.\)

Áp dụng

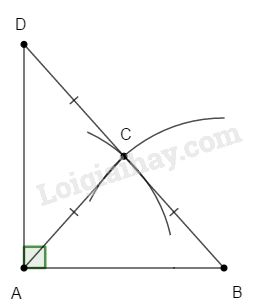
- Vẽ đường tròn \((A;r)\);  \(r > \dfrac{{AB}}{2}\); vẽ đường tròn \((B, r)\)

- Gọi \(C\) là giao điểm của \(2\) cung tròn nằm ở phía trong tờ giấy.

- Trên tia \(BC\) lấy \(D\) sao cho \(BC = CD\) \( \Rightarrow  AB  ⊥ AD.\)

Thật vậy: \(∆ABD\) có \(AC\) là trung tuyến ứng với \(BD\) (\(BD = CD\)) và \(AC = BC = CD\) (theo cách vẽ).

\( \Rightarrow  AC = \dfrac{1}{2} BD\) 

\( \Rightarrow   ∆ ABD\) vuông tại \(A.\)