Bài 64 trang 126 SGK Toán 6 tập 1
Giải bài 64 trang 126 SGK Toán 6 tập 1. cho hai đoạn thẳng AB dài 6cm. Gọi C là trung điểm của AB lấy D và E là hai điểm thuộc đoạn thẳng AB sao cho AD=BE=2cm. Vì sao C là trung điểm của DE?
Đề bài
Cho hai đoạn thẳng \(AB\) dài \(6cm\). Gọi \(C\) là trung điểm của \(AB\). Lấy \(D\) và \(E\) là hai điểm thuộc đoạn thẳng \(AB\) sao cho \(AD=BE=2cm\). Vì sao \(C\) là trung điểm của \(DE\)?
Phương pháp giải - Xem chi tiết
C là trung điểm của đoạn thẳng DE khi C nằm giữa D, E và cách đều D, E (CD = CE).
Lời giải chi tiết
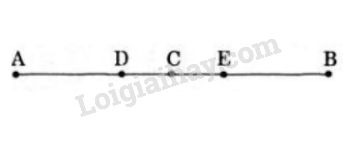
Vì \(C\) là trung điểm của \(AB\) nên \(C\) nằm giữa \(A\) và \(B\) và \(CA=CB= AB : 2 = 6:2 = 3(cm)\).
Trên tia \(AB\) có: \(AD < AC (2cm<3cm)\) nên điểm \(D\) nằm giữa \(A\) và \(C\), do đó \(CD=AC-AD=3 – 2 = 1 (cm)\).
Trên tia \(BA\) có: \(BE<BC\) nên điểm \(E\) nằm giữa \(B\) và \(C\) và \(CE=BC-BE=3-2=1cm\).
\(D\) nằm giữa \(A\) và \(C\) nên tia \(CD\) trùng với tia \(CA.\)
\(E\) nằm giữa \(B\) và \(C\) nên tia \(CE\) trùng với tia \(CB.\)
Tia \(CA\) và tia \(CB\) đối nhau nên tia \(CE\) và tia \(CD\) đối nhau. Do đó \(C\) nằm giữa \(D\) và \(E.\)
Mặt khác có \(CD=CE(=1cm)\) nên \(C\) là trung điểm của \(D\) và \(E.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 64 trang 126 SGK Toán 6 tập 1 timdapan.com"







