Bài 6 trang 75 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho tam giác ABC vuông cân tại A, điểm M thuộc cạnh BC và AM = m.
Đề bài
Cho tam giác ABC vuông cân tại A, điểm M thuộc cạnh BC và AM = m. Tính tổng \(M{B^2} + M{C^2}\) theo m.
Phương pháp giải - Xem chi tiết
Từ M kẻ ME vuông góc với AB, MF vuông góc với AC, áp dụng định lý Pythagore vào các tam giác vuông để tính \(M{B^2} + M{C^2}\) theo m.
Lời giải chi tiết
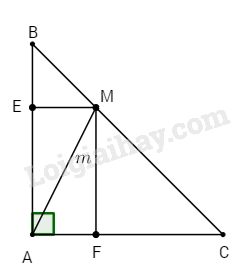
Từ M kẻ ME vuông góc với AB, MF vuông góc với AC.
Dễ thấy\( \Rightarrow \)\(\Delta EBM\) vuông cân tại E, \(\Delta FMC\) vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pythagore vào các tam giác EBM, FMC, AEF, ta có:
\(\begin{array}{l}M{B^2} = M{E^2} + B{E^2} = 2M{E^2}\\M{C^2} = M{F^2} + F{C^2} = 2M{F^2}\\ \Rightarrow M{B^2} + M{C^2} = 2\left( {M{E^2} + M{F^2}} \right)\,(1)\end{array}\)
Mà \(A{M^2} = E{F^2} = M{E^2} + M{F^2}\)(AEMF là hình chữ nhật) (2)
Từ (1) và (2) \( \Rightarrow M{B^2} + M{C^2} = 2A{M^2} = 2{m^2}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6 trang 75 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







