Bài 5 trang 127 SGK Hình học 10 nâng cao

Đề bài

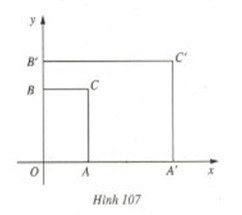
Trong mặt phẳng tọa độ Oxy cho hai hình chữ nhật OACB và OA’C’B’ như hình 107. Biết \(A(a\,;\,0)\,,\,{A'}({a'}\,;\,0)\,,\,B(0\,;\,b)\,,\,{B'}(0\,;\,{b'}\,)\,\) (a, a’, b, b; là những số dương, \(a\, \ne {a'}\,,\,b\, \ne \,{b'}\)).

a) Viết phương trình các đường thẳng AB’ và A’B.

b) Tìm liện hệ giữa để hai đường thẳng AB’ và A’B cắt nhau. Khi đó hãy tìm tọa độ giao điểm I của hai đường thẳng đó.

c) Chứng minh rằng ba điểm I, C, C’ thẳng hàng.

d) Với điều kiện nào của a, a’, b, b'; thì  C là trung điểm của IC’?

Lời giải chi tiết

a) Áp dụng phương trình đường thẳng theo đoạn chắn, ta có

\(A{B'}:\,\,{x \over a} + {y \over {{b'}}} = 1\,\,;\,\,\,\,{A'}B:\,\,{x \over {{a'}}} + {y \over b} = 1\)  

b) A'B và AB' cắt nhau \( \Leftrightarrow \,\,{a \over {{a'}}} \ne {{{b'}} \over b}\,\, \Leftrightarrow \,\,ab - {a'}{b'} \ne 0\) . Tọa độ giao điểm I của A'B và AB' là nghiệm của hệ phương trình:

\(\left\{ \matrix{
{b'}x + ay = a{b'} \hfill \cr 
bx + {a'}y = {a'}b \hfill \cr} \right.\,\, \Leftrightarrow \,\,\left\{ \matrix{
x = {{a{a'}\left( {{b'} - b} \right)} \over {{a'}{b'} - ab}} \hfill \cr 
y = {{b{b'}\left( {{a'} - a} \right)} \over {{a'}{b'} - ab}} \hfill \cr} \right.\)                  

Vậy \(I\left( {{{a{a'}\left( {{b'} - b} \right)} \over {{a'}{b'} - ab}};\,\,{{b{b'}\left( {{a'} - a} \right)} \over {{a'}{b'} - ab}}} \right)\)

c) Ta có \(C(a\,,\,b)\,;\,\,{C'}({a'}\,,\,{b'})\)

\(\overrightarrow {CI}  = \left( { - {{ab\left( {{a'} - a} \right)} \over {{a'}{b'} - ab}}; - {{ab\left( {{b'} - b} \right)} \over {{a'}{b'} - ab}}} \right) =  - {{ab} \over {{a'}{b'} - ab}}\overrightarrow {C{C'}} \)

Suy ra C, C', I  thẳng hàng.

d) C là trung điểm IC' .

\( \Leftrightarrow \,\,\overrightarrow {CI}  + \overrightarrow {C{C'}}  = \overrightarrow 0 \,\, \)

\(\Leftrightarrow \,\,\overrightarrow {CI}  =  - \overrightarrow {C{C'}} \,\, \Leftrightarrow \,\,{{ab} \over {{a'}{b'} - ab}} = 1\,\, \Leftrightarrow \,\,{a'}{b'} = 2ab\)