Bài 1 trang 126 SGK Hình học 10 nâng cao

Đề bài

Trên hình 105, ta có tam giác ABC và các hình vuông \(A{A'}{B_1}B,\,\,B{B'}{C_1}C,\,\,C{C'}{A_1}A\) .

Chứng  minh các đăng thức sau

a) \((\overrightarrow {A{A'}}  + \overrightarrow {B{B'}} ).\,\overrightarrow {AC}  = 0\)

b) \((\overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  + \overrightarrow {C{C'}} ).\,\overrightarrow {AC}  = 0\)

c) \(\overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  + \overrightarrow {C{C'}}  = 0\)

d) \(\overrightarrow {A{B_1}}  + \overrightarrow {B{C_1}}  + \overrightarrow {C{A_1}}  = 0\)

Lời giải chi tiết

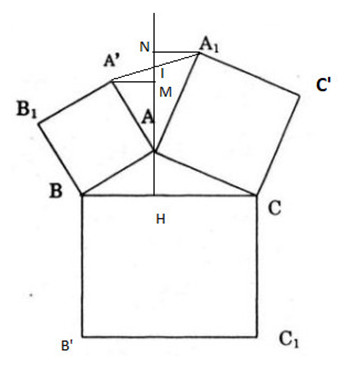
a) Kẻ \(AH \bot BC\) ta chứng minh đường thẳng AH cắt A’A₁ tại trung điểm I của A’A₁. Kẻ .

Ta có: \({A'}M \bot AH\,,\,\,{A_1}N \bot AH\)

\(\eqalign{
& \Delta AHB = \Delta {A'}MA\,\,\, \Rightarrow \,\,{A'}M = AH \cr 
& \Delta AHC = \Delta {A_1}NA\,\,\, \Rightarrow \,\,{A_1}N = AH \cr} \)                             

Từ đó suy ra: \(\Delta IM{A'} = \Delta IN{A_1}\,\,\, \Rightarrow \,\,I{A'} = \,\,I{A_1}\,\)

Tương tự gọi J là trung điểm \({B_1}{B'}\) thì \(BJ \bot AC\) .

Ta có           

\(\overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  = \overrightarrow {B{B_1}}  + \overrightarrow {B{B'}}  = 2\overrightarrow {BJ} \)

\(\Rightarrow \,\,(\overrightarrow {A{A'}}  + \overrightarrow {B{B'}} ).\,\overrightarrow {AC}  = 0\)               

b) Theo câu a) và \(\overrightarrow {C{C'}}  \bot \overrightarrow {AC} \) nên \((\overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  + \overrightarrow {C{C'}} ).\,\overrightarrow {AC}  = 0\) .

c) Đặt \(\overrightarrow u  = \overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  + \overrightarrow {C{C'}} \).

Ta có \(\overrightarrow u .\,\overrightarrow {AC}  = 0\,,\,\overrightarrow u .\,\overrightarrow {AB}  = 0\,\)  . Suy ra \(\overrightarrow u  = \overrightarrow 0 \) .

d) Ta có

\(\eqalign{
& \overrightarrow {A{B_1}} + \overrightarrow {B{C_1}} + \overrightarrow {C{A_1}}\cr& = \overrightarrow {A{A'}} + \overrightarrow {AB} + \overrightarrow {B{B'}} + \overrightarrow {BC} + \overrightarrow {C{C'}} + \overrightarrow {CA} \cr 
&  = \overrightarrow {A{A'}} + \overrightarrow {B{B'}} + \overrightarrow {C{C'}} + \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 \cr} \)