Bài 49 trang 84 SGK Toán 8 tập 2

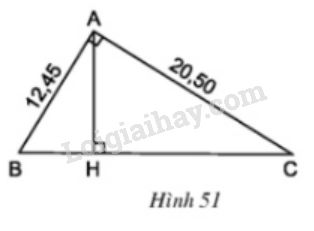
Ở hình 51, tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\)

LG a.

Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng?

Phương pháp giải:

Áp dụng:

- Trường hợp đồng dạng: Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia. 

Lời giải chi tiết:

Xét \(∆ABC \) và \( ∆HBA\) có:

\( \widehat{A} =  \widehat{H}={90^o}\)

\( \widehat{B}\) chung

\(\Rightarrow ∆ABC ∽ ∆HBA\) (g-g)

Xét \(∆ABC \) và \( ∆HAC\) có:

\( \widehat{A} = \widehat{H}={90^o}\)

\( \widehat{C}\) chung

\(\Rightarrow ∆ABC ∽ ∆HAC\) (g-g)

LG b.

Cho biết: \(AB = 12,45 cm\), \(AC = 20,50cm\). Tính độ dài các đoạn \(BC, AH, BH\) và \(CH.\)

Phương pháp giải:

Áp dụng:

- Tính chất hai tam giác đồng dạng và định lý Pytago

Lời giải chi tiết:

\(∆ABC\) vuông tại \(A\) (giả thiết) nên áp dụng định lí Pitago ta có:

\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr 
& \;\;\;\;\;\;\;\;= 12,{45^2} + 20,{50^2} = 575,2525 \cr 
& \Rightarrow BC = \sqrt {575,2525} \approx 24\,cm \cr} \)

\( ∆ABC ∽ ∆HBA \) (chứng minh trên)

\( \Rightarrow  \dfrac{AB}{HB} =  \dfrac{BC}{BA}\) 

\( \Rightarrow  HB =  \dfrac{AB^{2}}{BC} ≈  \dfrac{12,45^{2}}{24}≈ 6,5 cm\)

\( \Rightarrow CH = BC - BH \approx  24 - 6,5 \)\(\,= 17,5 cm.\) 

Mặt khác: \( \dfrac{AC}{AH} =  \dfrac{BC}{BA}\) (do \(∆ABC ∽ ∆HBA\) theo câu a)

\(\Rightarrow  AH = \dfrac{AB.AC}{BC}  \approx   \dfrac{12,45.20,50}{24}\) 

\( \Rightarrow  AH  \approx  10,6 cm\).