Bài 49 trang 135 SGK Đại số 10 nâng cao

Xét dấu các tam thức bậc hai sau:

LG a

3x² - 2x + 1

Phương pháp giải:

Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\)

Nếu \(\Delta  < 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \in \mathbb{R}\)

Nếu \(\Delta  = 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \ne  - \frac{b}{{2a}}\).

Nếu \(\Delta  > 0\) thì f(x) có hai nghiệm phân biệt \({x_1} < {x_2}\).

Khi đó trong khoảng hai nghiệm (\({x_1} < x < {x_2}\)) thì f(x) trái dấu với a, ngoài khoảng hai nghiệm (\(\left[ \begin{array}{l}x > {x_2}\\x < {x_1}\end{array} \right.\)) thì f(x) cùng dấu với a.

Lời giải chi tiết:

Ta có:

a = 3 > 0

Δ’ = 1 – 3 = -2 < 0

⇒ 3x² – 2x + 1 > 0,∀x  ∈ R

LG b

-x² + 4x – 1

Lời giải chi tiết:

Ta có:

a = -1 < 0

Δ’ = 4 – 1 = 3 > 0

Tam thức -x² + 4x – 1 có hai nghiệm phân biệt \(x = 2 \pm \sqrt 3 \)

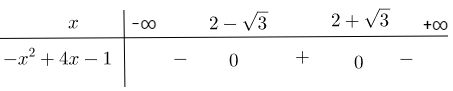
LG c

\({x^2} - \sqrt 3 x + {3 \over 4}\)

Lời giải chi tiết:

Ta có:

a = 1 > 0

Δ = 3 – 3 = 0

\({x^2} - \sqrt 3 x + {3 \over 4}\) có nghiệm kép \(x = {{\sqrt 3 } \over 2}\)

\( \Rightarrow {x^2} - \sqrt 3 x + {3 \over 4} > 0;\,\forall x \ne {{\sqrt 3 } \over 2}\)

LG d

\((1 - \sqrt 2 ){x^2} - 2x + 1 + \sqrt 2 \)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& a = 1 - \sqrt 2 < 0 \cr 
& (1 - \sqrt 2 ){x^2} - 2x + 1 + \sqrt 2 = 0 \cr&\Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr 
x = - 3 - 2\sqrt 2 \hfill \cr} \right. \cr} \)

Bảng xét dấu: