Bài 40 trang 62 SBT Hình học 12 Nâng cao

Một hình nón có bán kính R và chiều cao bằng 4R.

LG 1

Tính diện tích toàn phần của hình trụ nội tiếp hình nón, biết rằng bán kính đáy hình trụ bằng r. (Hình trụ được gọi là nội tiếp hình nón nếu một đường tròn đáy của hình trụ nằm trên mặt xung quanh của hình nón, đáy còn lại nằm trên mặt đáy của hình nón ).

Lời giải chi tiết:

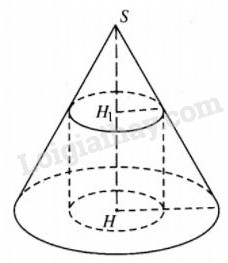
Dễ thấy \({r \over R} = {{S{H_1}} \over {SH}} = {{S{H_1}} \over {4R}} \Rightarrow S{H_1} = 4r\) và \(H{H_1} = 4\left( {R - r} \right).\)

Diện tích toàn phần của hình trụ nội tiếp hình nón tính theo r, R là

\({S_{tp}} = 2\pi {r^2} + 2\pi r.4\left( {R - r} \right) =  - 6\pi {r^2} + 8\pi Rr.\)

LG 2

Tính bán kính đáy r và chiều cao h của hình trụ nội tiếp hình nón để diện tích toàn phần của hình trụ đạt giá trị lớn nhất.

Lời giải chi tiết:

Vì chiều cao hình trụ là HH₁ được xác định bởi \(H{H_1} = 4\left( {R - r} \right)\) nên để tính bán kính r và chiều cao h của hình trụ nội tiếp hình nón sao cho diện tích toàn phần của hình trụ đó đạt giá trị lớn nhất, chỉ cần tìm r để \({S_{tp}} = 2\pi \left( { - 3{r^2} + 4Rr} \right)\) đạt giá trị lớn nhất ( với r < R). Khi coi r thay đổi thì

\(S{'_{tp}} = 2\pi \left( { - 6r + 4R} \right),\) từ đó

\(S{'_{tp}} = 0 \Leftrightarrow r = {2 \over 3}R.\)

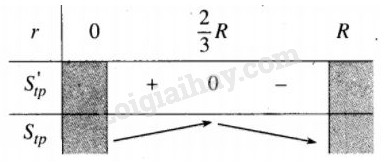
Vậy \({S_{tp}}\) đạt giá trị lớn nhất khi \(r = {2 \over 3}R.\)

Lúc đó \(h = 4\left( {R - {2 \over 3}R} \right) = {{4R} \over 3}.\)