Bài 39 trang 62 SBT Hình học 12 Nâng cao

Đề bài

Gọi (C ) là đường tròn chứa các điểm tiếp xúc của mặt xung quanh hình nón với mặt cầu nội tiếp hình nón đó. (C ) chia mặt xung quanh của hình nón thành hai phần. Hãy tính tỉ số diện tích hai phần đó biết diện tích hình cầu bằng diện tích đáy hình nón.

Lời giải chi tiết

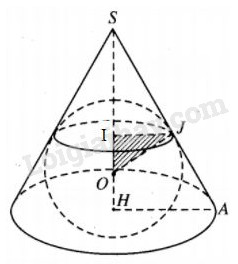
Kí hiệu bán kính đáy và chiều cao của hình nón lần lượt là x, y (x, y > 0), bán kính mặt cầu nội tiếp là r, dễ tính được

\(r = {{xy} \over {\sqrt {{x^2} + {y^2}}  + x}}.\)

Vì diện tích hình cầu bằng diện tích đáy hình nón nên ta có : \(4\pi {r^2} = \pi {x^2} \Leftrightarrow x = 2r,\) lúc đó

\(r = {{2ry} \over {\sqrt {{y^2} + 4{r^2}}  + 2r}} \Leftrightarrow r = {{3y} \over 8}.\)

Gọi IJ là bán kính của đường tròn (C ),

\(\Delta {\rm{IJ}}O\) \( \sim \Delta HSA\) (g.g), ta có

\({{{\rm{IJ}}} \over {HS}} = {{{\rm{OJ}}} \over {AS}} \Leftrightarrow IJ = {{SH.{\rm{OJ}}} \over {SA}} = {{y.r} \over {\sqrt {{y^2} + {x^2}} }}.\) Thay \(r = {{3y} \over 8},x = 2r\) vào hệ thức trên, ta được

\({\rm{IJ}} = {{y.{{3y} \over 8}} \over {\sqrt {{y^2} + {{9{y^2}} \over {16}}} }} = {{3y} \over {10}}.\)

Kí hiêu diện tích phần thứ nhất của mặt xung quanh hình nón ( phần có chứa đỉnh của hình nón ) là S₁ và diện tích xung quanh hình nón là \({S_{xq}}\) thì

\({{{S_1}} \over {{S_{xq}}}} = {\left( {{{{\rm{IJ}}} \over {HA}}} \right)^2} = {{{{\left( {{{3y} \over {10}}} \right)}^2}} \over {4{{\left( {{{3y} \over 8}} \right)}^2}}} = {4 \over {25}}.\)

Kí hiệu diện tích phần thứ hai của mặt xung quanh hình nón là \({S_2}\) thì

\({{{S_1}} \over {{S_2}}} = {1 \over {{{{S_2}} \over {{S_1}}}}} = {1 \over {{{{S_{xq}} - {S_1}} \over {{S_1}}}}} = {1 \over {{{25} \over 4} - 1}} = {4 \over {21}}.\)