Bài 36 trang 87 SGK Toán 6 tập 2

Đề bài

Cho hai tia \(Oy,Oz\) cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox.\) Biết: \(\widehat{ xOy}=30^0,\) \(\widehat{ xOz}=80^0.\) Vẽ tia phân giác \(Om\) của \(\widehat {xOy}\). Vẽ tia phân giác \(On\) của \(\widehat {yOz}\). Tính \(\widehat {mOn}\) 

Lời giải chi tiết

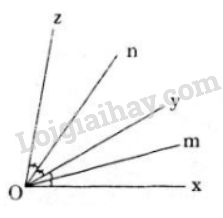
Vì hai tia \(Oy, Oz\) cùng nằm trên nửa mặt phẳng bờ chứa tia \(Ox\) mà 

\(\widehat{ xOy}\)<  \(\widehat{ xOz}\) \((30^0<80^0)\) nên tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)

Do đó  \(\widehat{ xOy}\)+ \(\widehat{ yOz}\)= \(\widehat{ xOz}\)  

Suy ra  \(\widehat{ yOz}=\widehat{ xOz}-\widehat{ xOy}\)\(= 80^0-30^0=50^0\) 

Ta có tia \(Om\) là tia phân giác của góc \(xOy\) nên: \(\widehat {xOm} = \widehat {mOy} \)\(= \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{30}^0}}}{2} = {15^0}\)

Tia \(On\) là tia phân giác của góc \(yOz\) nên: \(\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} \)\(= \dfrac{{{{50}^0}}}{2} = {25^0}\)

Vì tia \(Oy\) nằm giữa hai tia \(Ox,Oz\) mà tia \(On\) là tia phân giác góc \(zOy\), tia \(Om\) là tia phân giác góc \(xOy\) nên \(Om\) và \(On\) nằm trên hai nửa mặt phẳng đối nhau bờ là tia \(Oy\). Do đó tia \(Oy\) nằm giữa hai tia \(Om, On\), suy ra: 

\(\widehat{mOn}\) =\(\widehat{mOy}\) + \(\widehat{yOn}\) \( = {15^0} + {25^0} = {40^0}\)