Bài 31 trang 59 SGK Đại số 10 nâng cao

Hàm số \(y{\rm{ }} = {\rm{ }} - 2{x^2} - {\rm{ }}4x{\rm{ }} + {\rm{ }}6\) có đồ thị là Parabol (P).

LG a

Tìm tọa độ đỉnh, phương trình trục đối xứng của (P).

Giải chi tiết:

Ta có: a = -2; b = -4; c = 6

\(\eqalign{
& {x_0} = {{ - b} \over {2a}} = {4 \over { - 4}} = - 1 \cr 
& \Rightarrow {y_0} = - 2{( - 1)^2} - 4( - 1) + 6 = 8 \cr} \)

Tọa độ đỉnh (P) là: \(I = (-1; 8)\)

Phương trình trục đối xứng của (P) là: \(x = -1\)

LG b

Vẽ Parabol (P).

Giải chi tiết:

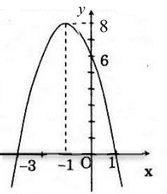
Đồ thị (P): 

Giao đồ thị với \(Ox\) :

\(y = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr 
x = - 3 \hfill \cr} \right.\)

LG c

Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0

Giải chi tiết:

Ta có:

\(y ≥ 0 ⇔ -3 ≤ x ≤ 1\)