Bài 30 trang 114 SGK Toán 8 tập 2

Đề bài

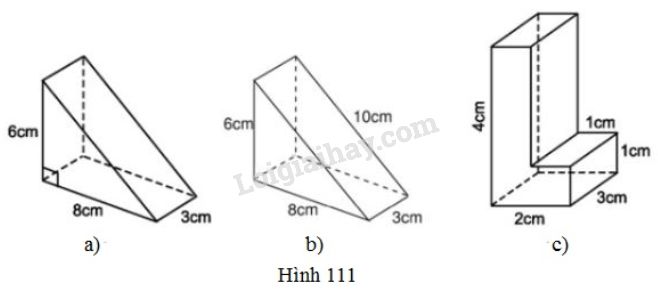
Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.

Lời giải chi tiết

+) Hình a là lăng trụ đứng có chiều cao là \(3cm\) và đáy là tam giác vuông có hai cạnh góc vuông là \(6cm,\; 8cm\). 

Suy ra cạnh huyền là \(\sqrt{6^{2}+8^{2}} = \sqrt{36+64} = \sqrt{100} = 10\) \((cm)\).

Diện tích đáy là :  \(S = \dfrac{1}{2}6 . 8 = 24(cm^2) \)

Thể tích lăng trụ là: \(V = S.h = 24.3 = 72(cm^3) \)

Diện tích xung quanh lăng trụ là:

          \(S_{xq} =2p.h = (6+8+10).3 = 24.3 \)\(=72 \) \((cm^2)\)

Diện tích toàn phần lăng trụ là:

          \(S_{tp} =S_{xq}+2. S_{đ} = 72 +2.24 =120\) \((cm^2)\)

+) Hình b là lăng trụ đứng tam giác có ba kích thước là \(6cm,\, 8cm, \,10cm\); chiều cao lăng trụ là \(3cm\).

Vì \(6^2 + 8^2 = 36 + 64 = 100 = 10^2 \) nên đáy lăng trụ là tam giác vuông có hai cạnh góc vuông là \(6cm,\, 8cm\). Do đó, bài toán này quay về bài toán ở hình a, ta thu được kết quả:

         \(V= 72cm^3; \quad S_{xq} = 72 cm^2;\)\( \quad S_{tp} =120(cm^2)\).

+) Hình c là hình gồm hai lăng trụ đứng: Hình lăng trụ một là hình hộp chữ nhật có các kích thước \(4cm, \; 1cm,\; 3cm\) ; hình lăng trụ hai là hình hộp chữ nhật có các kích thước \(1cm,\;1cm, \; 3cm\).

Thể tích lăng trụ một là:      \( V_1 = 4.1.3 =12 (cm^3)\)

Thể tích lăng trụ hai là:       \( V_2 = 1.1.3 =3 (cm^3)\)

Thể tích lăng trụ đã cho là

        \( V = V_1+ V_2 = 12 +3 =15 (cm^3)\)

Diện tích xung quanh của lăng trụ một là:

       \( S_{xq1} = 2.(3+1).4 =32 (cm^2)\)

Diện tích một đáy của lăng trụ một là:

       \( S_{đ1} = 3.1 =3 (cm^2) \)

Diện tích toàn phần của lăng trụ một là:

         \( S_{tp1} =S_{xq1} +2. S_{đ1} = 32 +2.3 =38 \) \((cm^2)\)

Diện tích xung quanh của lăng trụ hai là:

        \( S_{xq2} = 2.(1+3).1 =8 (cm^2)\)

Diện tích một đáy của lăng trụ hai là:

       \( S_{đ2} = 3.1 =3 (cm^2) \)

Diện tích toàn phần của lăng trụ hai là:

        \( S_{tp2} =S_{xq2} +2. S_{đ2} = 8 +2.3=14\) \( (cm^2)\)

Diện tích toàn phần của lăng trụ đã cho bằng tổng diện tích toàn phần của lặng trụ 1 và 2 trừ đi 2 phần diện tích chung là hình chữ nhật với các kích thước \(1cm,\; 3cm\). Do đó:

        \( S_{tp} =S_{tp1} +S_{tp2} - 2. S_{hcn} \) 

                    \(=38 + 14 - 2.3.1 =46 (cm^2)\)