Bài 3 trang 113 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung nhỏ AC lấy một điểm D. Trên dây cung BD lấy điểm M sao cho DM = DC.

a) Chứng minh MCD là tam giác đều.

b) Khi điểm D di động trên cung nhỏ AC (D có thể trùng điểm A hoặc điểm C), tập hợp các điểm M là gì?

Lời giải chi tiết

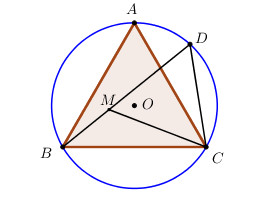
a) Ta có: \(\widehat {CDM} = \widehat {CAB} = {60^0}\) (2 góc nội tiếp cùng chắn cung BC).

Xét tam giác MCD có: \(\left\{ \begin{array}{l}MC = MD\,\,\left( {gt} \right)\\\widehat {CDM} = {60^0}\,\left( {cmt} \right)\end{array} \right. \Rightarrow \Delta MCD\) đều.

b) Do tam giác MCD đều (cmt) \( \Rightarrow \widehat {CMD} = {60^0}\).

Mà \(\widehat {CMD} + \widehat {BMC} = {180^0}\) (2 góc kề bù)

\( \Rightarrow \widehat {BMC} = {180^0} - \widehat {CMD}\)\(\; = {180^0} - {60^0} = {120^0}\).

B, C cố định, do đó M thuộc cung chứa góc 120⁰ dựng trên đoạn thẳng BC.

Giới hạn: Khi \(D \equiv B \Rightarrow M \equiv B;\,\,D \equiv C \Rightarrow M \equiv C\).

Vậy tập hợp các điểm M là cung chứa góc 120⁰ dựng trên đoạn thẳng BC cùng phía với điểm A.