Bài 25 trang 123 SGK Toán 8 tập 1

Đề bài

Tính diện tích của một tam giác đều có cạnh là \(a.\)

Lời giải chi tiết

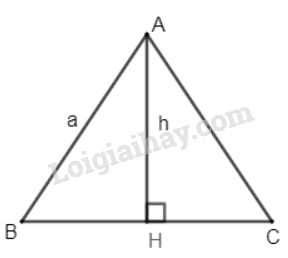
Gọi \(h\) là chiều cao của tam giác đều cạnh \(a\)

Tam giác \(ABC\) đều cạnh \(a\) có \(AH\) vừa là đường cao đồng thời là trung tuyến ứng với cạnh \(BC\) (tính chất tam giác đều).

Do đó \(H\) là trung điểm của \(BC\).

Hay \(BH = \dfrac{1}{2}BC = \dfrac{a}{2}\)

Áp dụng định lí Pitago vào tam giác vuông \(ABH\) ta có:

\(A{H^2} = A{B^2} - B{H^2}\)

\({h^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3{a^2}}}{4}\)

\( \Rightarrow h = \dfrac{{a\sqrt 3 }}{2}\)

Vậy \(S _{ABC}= \dfrac{1}{2}ah = \dfrac{1}{2}a.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4}\)