Bài 24 Trang 162 SGK Đại số và Giải tích 12 Nâng cao

Tính các tích phân sau :

LG a

\(\int\limits_1^2 {{x^2}{e^{{x^3}}}dx;} \)

Phương pháp giải:

Đổi biến \(u=x^3\)

Lời giải chi tiết:

Đặt \(u = {x^3} \Rightarrow du = 3{x^2}dx \Rightarrow {x^2}dx = {{du} \over 3}\) 

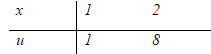
\(\int\limits_1^2 {{x^2}{e^{{x^3}}}dx = {1 \over 3}} \int\limits_1^8 {{e^u}du }\) \(= \left. {{1 \over 3}{e^u}} \right|_1^8  = {1 \over 3}\left( {{e^8} - e} \right)\)

LG b

\(\int\limits_1^3 {{1 \over x}} {\left( {\ln x} \right)^2}dx;\) 

Phương pháp giải:

Đổi biến u=lnx

Lời giải chi tiết:

Đặt \(u = \ln x \Rightarrow du = {{dx} \over x}\)

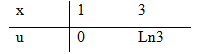
\(\int\limits_1^3 {{1 \over x}} {\left( {\ln x} \right)^2}dx = \int\limits_0^{\ln 3} {{u^2}du }\) \(= \left. {{{{u^3}} \over 3}} \right| _0^{\ln 3} = {1 \over 3}{\left( {\ln 3} \right)^3}\)

LG c

\(\int\limits_0^{\sqrt 3 } {x\sqrt {1 + {x^2}} } dx;\)

Phương pháp giải:

Đổi biến \(u = \sqrt {1 + {x^2}}\)

Lời giải chi tiết:

Đặt \(u = \sqrt {1 + {x^2}}  \Rightarrow {u^2} = 1 + {x^2} \) \(\Rightarrow udu = xdx\)

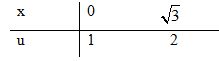
\(\int\limits_0^{\sqrt 3 } {x\sqrt {1 + {x^2}} } dx = \int\limits_1^2 {u.udu }\) \( = \int\limits_1^2 {{u^2}du} = \left. {{{{u^3}} \over 3}} \right| _1^2 = {7 \over 3}\)

LG d

\(\int\limits_0^1 {{x^2}{e^{3{x^3}}}dx;} \)

Phương pháp giải:

Đổi biến \(u = 3{x^3}\)

Lời giải chi tiết:

 Đặt \(u = 3{x^3} \Rightarrow du = 9{x^2}dx \) \(\Rightarrow {x^2}dx = {1 \over 9}du\)

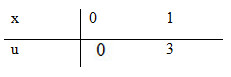
\(\int\limits_0^1 {{x^2}{e^{3{x^3}}}dx = {1 \over 9}} \int\limits_0^3 {{e^u}du}  \) \(= \left. {{1 \over 9}{e^u}} \right|_0^3 = {1 \over 9}\left( {{e^3} - 1} \right)\) 

LG e

\(\int\limits_0^{{\pi  \over 2}} {{{\cos x} \over {1 + {\mathop{\rm s}\nolimits} {\rm{inx}}}}} dx.\) 

Lời giải chi tiết:

Đặt \(u = 1 + {\mathop{\rm s}\nolimits} {\rm{inx}} \Rightarrow du = \cos xdx\)

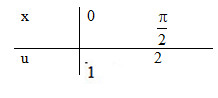
\(\int\limits_0^{{\pi  \over 2}} {{{\cos xdx} \over {1 + {\mathop{\rm s}\nolimits} {\rm{inx}}}}}  = \int\limits_1^2 {{{du} \over u}}  = \left. {\ln \left| u \right|} \right|_1^2 = \ln 2\)