Bài 2 trang 45 SGK Hình học 10

Cho ba điểm \(O, A, B\) thẳng hàng biết \(OA = a, OB = b\). Tính tích vô hướng của \(\vec{OA}\).\(\vec{OB}\) trong \(2\) trường hợp

LG a

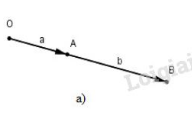
Điểm \(O\) nằm ngoài đoạn \(AB.\)

Phương pháp giải:

Cho hai vecto \(\overrightarrow a\) và \( \overrightarrow b \) đều khác vecto \( \overrightarrow 0. \) Khi đó tích vô hướng của vecto \(\overrightarrow a\) và \( \overrightarrow b \) được xác định bởi công thức sau:

\[\overrightarrow a \overrightarrow {.b}  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\]

Lời giải chi tiết:

Khi \(O\) nằm ngoài đoạn \(AB\) thì  hai vec tơ \(\vec{OA}\) và \(\vec{OB}\) cùng hướng và góc \((\vec{OA}, \vec{OB}) = 0^0 \Rightarrow \cos(\vec{OA}, \vec{OB}) = 1\)   nên  \(\vec{OA}.\vec{OB} = a.b.\)

LG b

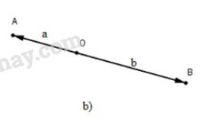
Điểm \(O\) nằm trong đoạn \(AB.\)

Phương pháp giải:

Cho hai vecto \(\overrightarrow a\) và \( \overrightarrow b \) đều khác vecto \( \overrightarrow 0. \) Khi đó tích vô hướng của vecto \(\overrightarrow a\) và \( \overrightarrow b \) được xác định bởi công thức sau:

\[\overrightarrow a \overrightarrow {.b}  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\;\overrightarrow b } \right).\]

Lời giải chi tiết:

Khi \(O\) nằm trong đoạn \(AB\) thì  hai vectơ \(\vec{OA}\) và \(\vec{OB}\) ngược hướng và góc \( (\vec{OA}, \vec{OB}) = 180^0 \)\(\Rightarrow \cos( \vec{OA}, \vec{OB}) = -1\)   nên  \(\vec{OA}.\vec{OB} = -a.b.\)