Bài 12 trang 46 SGK Đại số 10 nâng cao

Khảo sát sự biến thiên của các hàm số sau

LG a

\(y = {1 \over {x - 2}}\) trên mỗi khoảng \((-∞; 2)\) và \((2; +∞)\)

Giải chi tiết:

\(f(x) = {1 \over {x - 2}}\)

+ Với x₁; x₂ ∈ \((-∞; 2)\) và x₁ ≠ x₂; ta có:

 \(f({x_2}) - f({x_1}) = {1 \over {{x_2} - 2}} - {1 \over {{x_1} - 2}} = {{{x_1} - 2 - {x_2} + 2} \over {({x_1} - 2)({x_2} - 2)}}\)

\(= {{{x_1} - {x_2}} \over {({x_1} - 2)({x_2} - 2)}}\)

\( \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {{ - 1} \over {({x_1} - 2)({x_2} - 2)}} < 0\) 

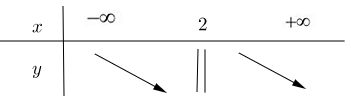
Vậy hàm số \(y = {1 \over {x - 2}}\) nghịch biến trên \((-∞; 2)\)

+ Với x₁; x₂ ∈ \((2; +∞)\) và x₁ ≠ x₂; ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {{ - 1} \over {({x_1} - 2)({x_2} - 2)}} < 0\)

Vậy hàm số \(y = {1 \over {x - 2}}\)  nghịch biến trên \((2; +∞)\)

Bảng biến thiên

LG b

y = x² – 6x + 5 trên mỗi khoảng \((-∞; 3)\) và \((3; +∞)\)

Giải chi tiết:

 f(x) = x² – 6x + 5

+ Với x₁; x₂ ∈ \((-∞; 3)\)  và x₁ ≠ x₂; ta có:

f(x₂) – f(x₁) = x₂² – 6x₂ + 5 – (x₁² – 6x₁ + 5)

= x₂² - x₁² + 6(x₁ – x₂) = (x₂ – x₁)(x₁  + x₂ – 6)

\( \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {x_1} + {x_2} - 6 < 0\)  (vì x₁ < 3; x₂ < 3)

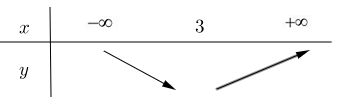
Vậy hàm số y = x² – 6x + 5 nghịch biến trên \((-∞, 3)\) 

+ Với x₁; x₂ ∈ \((3, +∞)\) và x₁ ≠ x₂; ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {x_1} + {x_2} - 6 > 0\) (vì x₁ > 3; x₂ > 3)

Vậy hàm số y = x² – 6x + 5 đồng biến trên \((3;+∞)\) 

Bảng biến thiên

LG c

y = x²⁰⁰⁵ + 1 trênn khoảng \((-∞; +∞)\)

Giải chi tiết:

Với mọi x₁, x₂ ∈ \((-∞; +∞)\) , ta có x₁ < x₂ 

\(\Rightarrow\) x₁²⁰⁰⁵ < x₂²⁰⁰⁵

\(\Rightarrow\)  x₁²⁰⁰⁵ + 1 < x₂²⁰⁰⁵ + 1

hay f(x₁) < f(x₂) (y = f(x) = x²⁰⁰⁵ + 1).

Từ đấy ta có, hàm số đã cho đồng biến trên \((-∞; +∞)\)