Bài 14: Mạch có R, L, C mắc nối tiếp
Video bài giảng
1. Phương pháp giản đồ Fre-nen
a. Định luật về điện áp tức thời
-
Trong mạch điện xoay chiều gồm nhiều đọan mạch mắc nối tiếp thì điện áp tức thời giữa hai đầu của mạch bằng tổng đại số các điện áp tức thời giữa hai đầu của từng đọan mạch ấy
\(u=u_1+u_2+u_3+...\)
b. Phương pháp giản đồ Fre-nen
-
Biểu diễn riêng từng điện áp \(U_R;U_L;U_C\)
\(u_R=U_{0R}cos(\omega t+\varphi_i )\)
⇒ \(U_{R}\) và i cùng pha .

\(u_L=U_{0L}cos(\omega t+\varphi_i +\frac{\pi }{2})\)
=> \(U_{L}\) sớm pha \(\frac{\pi }{2}\) so với i .

\(u_C=U_{0C}cos(\omega t+\varphi_i -\frac{\pi }{2})\)
=> \(U_{C}\) chậm (trễ) pha \(\frac{\pi }{2}\) so với i .

-
Trong đó:
-
\(U_R\) = I.R: điện áp hiệu dụng giữa hai đầu điện trở R (V)
-
\(U_L\) = I.\(Z_L\): điện áp hiệu dụng giữa hai đầu cuộn cảm L (V)
-
\(U_C\) = I.\(Z_C\): điện áp hiệu dụng giữa hai đầu tụ điện C (V)
-
U = I.Z: điện áp hiệu dụng giữa hai đầu đoạn mạch R, L, C mắc nối tiếp (V)
-
2. Mạch có R, L, C mắc nối tiếp
- Sơ đồ mạch điện R,L,C mắc nối tiếp:
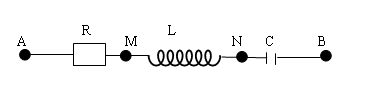
a. Định luật Ohm cho đọan mạch có R, L, C mắc nối tiếp. Tổng trở.
- Giả sử cho dòng điện trong đọan mạch có biểu thức
\(i=I_0.cos\omega t\)
- Điện áp tức thời đọan mạch AB:
\(u_{AB}=U_0.cos(\omega t+\varphi )\)
\(u_{AB}=U_R+U_L+U_C\)
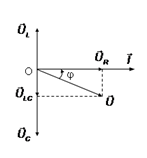
Giản đồ Fre- nen :
- Trường hợp 1: \(U_L> U_C(Z_L> Z_C)\)
Phương pháp giản đồ Fre-nen
\(\underset{u_{AB}}{\rightarrow}=\underset{U_R}{\rightarrow}+\underset{U_L}{\rightarrow}+\underset{U_C}{\rightarrow}\)
\(u_{AB}^{2}=U_R^{2}+(U_L-U_C)^{2}\)
\(Z_{AB}=\sqrt{R^{2}+(Z_L-Z_C)^{2}}\)
\(I=\frac{U_{AB}}{Z_{AB}}\)
|
Bài 1:
Mạch điện xoay chiều gồm một điện trở thuần R = 50\(\Omega\), một cuộn thuần cảm có hệ số tự cảm \(L=\frac{1}{\pi }(H)\) và một tụ điện có điện dung \(C=\frac{2.10^{-4}}{\pi }(F)\) mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng \(i=5cos(100\pi t)(A)\).Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.
Hướng dẫn giải:
Cảm kháng: \(Z_L=\omega L=100\pi.\frac{1}{\pi }=100\Omega\)
Dung kháng: \(Z_C=\frac{1}{\omega C}=\frac{1}{100\pi.\frac{2.10^{-4}}{\pi }}=50\Omega\)
Tổng trở:
\(\begin{array}{l}
Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\
= \sqrt {{{50}^2} + {{(100 - 50)}^2}} = 50\sqrt 2 \Omega
\end{array}\)
Độ lệch pha giữa u hai đầu mạch và i:
\(\begin{array}{l}
tan\varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{100 - 50}}{{50}}\\
\Leftrightarrow tan\varphi = 1\\
\Rightarrow \varphi = \frac{\pi }{4}(rad)
\end{array}\)
Biểu thức điện áp tức thời giữa hai đầu mạch điện:
\(u=250\sqrt{2}cos(100\pi t+\frac{\pi }{4})(V)\)
Bài 2:
Một mạch điện xoay chiều RLC không phân nhánh có R = 100\(\Omega\); \(C=\frac{1.10^{-4}}{\pi }(F)\);\(L=\frac{2}{\pi }(H)\) . Cường độ dòng điện qua mạch có dạng: \(i=2cos(100\pi t)(A)\). Viết biểu thức tức thời điện áp của hai đầu mạch .
Hướng dẫn giải:
Cảm kháng: \(Z_L=\omega L=100\pi.\frac{2}{\pi }=200\Omega\)
Dung kháng:
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{1.10}^{ - 4}}}}{\pi }}} = 100\Omega \)
Tổng trở:
\(\begin{array}{l}
Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\
= \sqrt {{{100}^2} + {{(200 - 100)}^2}} = 100\sqrt 2 \Omega
\end{array}\)
Hiệu điện thế cực đại:
\(U_0=I_0.Z= 2.100\sqrt{2}=200\sqrt{2}(V)\)
Độ lệch pha :
\(\begin{array}{l}
tan\varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{200 - 100}}{{100}} = \\
\Leftrightarrow tan\varphi = 1\\
\Rightarrow \varphi = \frac{\pi }{4}(rad)
\end{array}\)
Pha ban đầu của HĐT:
\(\varphi _u=\varphi _i+\varphi =0+\frac{\pi }{4}=\frac{\pi }{4}\)
⇒ Biểu thức tức thời điện áp của hai đầu mạch:
\(\begin{array}{l}
u = {U_0}cos(\omega t + {\varphi _u})\\
= 200\sqrt 2 cos(100\pi t + \frac{\pi }{4})(V)
\end{array}\)
1. Phương pháp giản đồ Fre-nen
a. Định luật về điện áp tức thời
-
Trong mạch điện xoay chiều gồm nhiều đọan mạch mắc nối tiếp thì điện áp tức thời giữa hai đầu của mạch bằng tổng đại số các điện áp tức thời giữa hai đầu của từng đọan mạch ấy
\(u=u_1+u_2+u_3+...\)
b. Phương pháp giản đồ Fre-nen
-
Biểu diễn riêng từng điện áp \(U_R;U_L;U_C\)
\(u_R=U_{0R}cos(\omega t+\varphi_i )\)
⇒ \(U_{R}\) và i cùng pha .

\(u_L=U_{0L}cos(\omega t+\varphi_i +\frac{\pi }{2})\)
=> \(U_{L}\) sớm pha \(\frac{\pi }{2}\) so với i .

\(u_C=U_{0C}cos(\omega t+\varphi_i -\frac{\pi }{2})\)
=> \(U_{C}\) chậm (trễ) pha \(\frac{\pi }{2}\) so với i .

-
Trong đó:
-
\(U_R\) = I.R: điện áp hiệu dụng giữa hai đầu điện trở R (V)
-
\(U_L\) = I.\(Z_L\): điện áp hiệu dụng giữa hai đầu cuộn cảm L (V)
-
\(U_C\) = I.\(Z_C\): điện áp hiệu dụng giữa hai đầu tụ điện C (V)
-
U = I.Z: điện áp hiệu dụng giữa hai đầu đoạn mạch R, L, C mắc nối tiếp (V)
-
2. Mạch có R, L, C mắc nối tiếp
- Sơ đồ mạch điện R,L,C mắc nối tiếp:

a. Định luật Ohm cho đọan mạch có R, L, C mắc nối tiếp. Tổng trở.
- Giả sử cho dòng điện trong đọan mạch có biểu thức
\(i=I_0.cos\omega t\)
- Điện áp tức thời đọan mạch AB:
\(u_{AB}=U_0.cos(\omega t+\varphi )\)
\(u_{AB}=U_R+U_L+U_C\)
Giản đồ Fre- nen :
- Trường hợp 1: \(U_L> U_C(Z_L> Z_C)\)
Phương pháp giản đồ Fre-nen
\(\underset{u_{AB}}{\rightarrow}=\underset{U_R}{\rightarrow}+\underset{U_L}{\rightarrow}+\underset{U_C}{\rightarrow}\)
\(u_{AB}^{2}=U_R^{2}+(U_L-U_C)^{2}\)
\(Z_{AB}=\sqrt{R^{2}+(Z_L-Z_C)^{2}}\)
\(I=\frac{U_{AB}}{Z_{AB}}\)
|
Bài 1:
Mạch điện xoay chiều gồm một điện trở thuần R = 50\(\Omega\), một cuộn thuần cảm có hệ số tự cảm \(L=\frac{1}{\pi }(H)\) và một tụ điện có điện dung \(C=\frac{2.10^{-4}}{\pi }(F)\) mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng \(i=5cos(100\pi t)(A)\).Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.
Hướng dẫn giải:
Cảm kháng: \(Z_L=\omega L=100\pi.\frac{1}{\pi }=100\Omega\)
Dung kháng: \(Z_C=\frac{1}{\omega C}=\frac{1}{100\pi.\frac{2.10^{-4}}{\pi }}=50\Omega\)
Tổng trở:
\(\begin{array}{l}
Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\
= \sqrt {{{50}^2} + {{(100 - 50)}^2}} = 50\sqrt 2 \Omega
\end{array}\)
Độ lệch pha giữa u hai đầu mạch và i:
\(\begin{array}{l}
tan\varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{100 - 50}}{{50}}\\
\Leftrightarrow tan\varphi = 1\\
\Rightarrow \varphi = \frac{\pi }{4}(rad)
\end{array}\)
Biểu thức điện áp tức thời giữa hai đầu mạch điện:
\(u=250\sqrt{2}cos(100\pi t+\frac{\pi }{4})(V)\)
Bài 2:
Một mạch điện xoay chiều RLC không phân nhánh có R = 100\(\Omega\); \(C=\frac{1.10^{-4}}{\pi }(F)\);\(L=\frac{2}{\pi }(H)\) . Cường độ dòng điện qua mạch có dạng: \(i=2cos(100\pi t)(A)\). Viết biểu thức tức thời điện áp của hai đầu mạch .
Hướng dẫn giải:
Cảm kháng: \(Z_L=\omega L=100\pi.\frac{2}{\pi }=200\Omega\)
Dung kháng:
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{1.10}^{ - 4}}}}{\pi }}} = 100\Omega \)
Tổng trở:
\(\begin{array}{l}
Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\
= \sqrt {{{100}^2} + {{(200 - 100)}^2}} = 100\sqrt 2 \Omega
\end{array}\)
Hiệu điện thế cực đại:
\(U_0=I_0.Z= 2.100\sqrt{2}=200\sqrt{2}(V)\)
Độ lệch pha :
\(\begin{array}{l}
tan\varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{200 - 100}}{{100}} = \\
\Leftrightarrow tan\varphi = 1\\
\Rightarrow \varphi = \frac{\pi }{4}(rad)
\end{array}\)
Pha ban đầu của HĐT:
\(\varphi _u=\varphi _i+\varphi =0+\frac{\pi }{4}=\frac{\pi }{4}\)
⇒ Biểu thức tức thời điện áp của hai đầu mạch:
\(\begin{array}{l}
u = {U_0}cos(\omega t + {\varphi _u})\\
= 200\sqrt 2 cos(100\pi t + \frac{\pi }{4})(V)
\end{array}\)
.PNG)