Bài 12: Đại cương về dòng điện xoay chiều
Video bài giảng
1. Khái niệm về dòng điện xoay chiều
-
Là dòng điện có cường độ biến thiên tuần hoàn với thời gian theo quy luật của hàm số sin hay cosin, với dạng tổng quát:
\(i=I_0cos(\omega t+\varphi )\)
-
Trong đó:
-
\(i\): giá trị của cđdđ tại thời điểm t, (cường độ tức thời).
-
\(I_0\) > 0: giá trị cực đại (cường độ cực đại).
-
\(\omega\) > 0: tần số góc (rad/s)
-
\(\omega =2\pi f=\frac{2\pi }{T}\)
-
\(f:\) tần số (Hz), T: chu kì (s)
-
\((\omega t+\varphi )\) pha của i (rad)
-
\(\varphi\) pha ban đầu (rad)
-
2. Nguyên tắc tạo ra dòng điện xoay chiều
a. Nguyên tắc:
-
Khi cho một khung dây quay đều trong từ trường đều thì trong khung dây xuất hiện suất điện động cảm ứng xoay chiều. Nếu nối hai đầu khung dây với một mạch ngoài kín thì trong mạch ngoài có dòng điện xoay chiều.
b. Khảo sát lý thuyết:
-
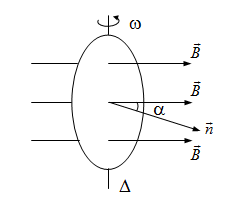
Xét một cuộn dây dẫn dẹt hình tròn, khép kín, quay quanh trục cố định đồng phẳng với cuộn dây đặt trong từ trường đều \(\underset{B}{\rightarrow}\) có phương vuông góc với trục quay.
-
Giả sử lúc t = 0, \(\alpha\) = 0
-
Lúc \(t> 0\rightarrow \alpha =\omega t\) , từ thông qua cuộn dây:
\(\phi =NBScos\alpha =NBScos\omega t\).
-
Vì \(\phi\) biến thiên theo thời gian t nên trong cuộn dây xuất hiện suất điện động cảm ứng:
\(e=-\frac{d\phi }{dt}=NBS\omega sin\omega t\)
-
Nếu cuộn dây kín có điện trở R thì cường độ dòng điện cảm ứng cho bởi:
3. Giá trị hiệu dụng
a. Cường độ hiệu dụng I
Cho dòng điện xoay chiều:
-
\(i=I_0cos(\omega t+\varphi )\) chạy qua điện trở R
-
Công suất tức thời tiêu thụ trong R:
\(p=Ri^2=R.I_{0}^{2}.cos^{2}(\omega t+\varphi )\)
-
Giá trị trung bình của p trong một chu kì là công suất trung bình:
\(\begin{array}{l}
P = p = RI_0^2co{s^2}\omega t\\
\Rightarrow P = p = \frac{1}{2}RI_0^2
\end{array}\)
Đặt:
-
\(I=\frac{I_0}{\sqrt{2}}\)
-
\(P=RI^2\)
-
\(I\): là giá trị hiệu dụng của cường độ dòng điện xoay chiều (cường độ hiệu dụng).
-
\(I_0\): cường độ cực đại.
Định nghĩa: Cường độ hiệu dụng của dòng điện xoay chiều là đại lượng có giá trị bằng cường độ của một dòng điện không đổi, sao cho khi đi qua cùng một điện trở R thì công suất tiêu thụ trong R bởi 2 dòng điện đó là như nhau.
b. Hiệu điện thế, suất điện động hiệu dụng
\(\begin{array}{l} U = \frac{{{U_0}}}{{\sqrt 2 }};\\ I = \frac{{{I_0}}}{{\sqrt 2 }} \end{array}\)
c. Chú ý
-
Số liệu ghi trên các thiết bị điện đều là các giá trị hiệu dụng.
-
Các thiết bị đo đối với mạch điện xoay chiều đo giá trị hiệu dụng.
Bài 1:
Xác định giá trị cực đại, tần số góc, chu kì, tần số, pha ban đầu của các dòng điện xoay chiều có cường độ tức thời cho bởi :
a. \(i=5cos(100\pi t+\frac{\pi }{4}) (A)\)
b. \(i=-5\sqrt{2}cos100\pi t (A)\)
Hướng dẫn giải :
a.
\(\begin{array}{l}
i = 5cos(100\pi t + \frac{\pi }{4})(A)\\
\to {I_0} = 5A;\\
\omega = 100\pi t(rad/s);\\
T = \frac{{2\pi }}{\omega } = 0,02(s);\\
f = \frac{1}{T} = 50(Hz);\\
\varphi = \frac{\pi }{4}(rad)
\end{array}\)
b.
\(\begin{array}{l}
i = - 5\sqrt 2 cos100\pi t(A)\\
\Leftrightarrow i = 5\sqrt 2 cos(100\pi t + \pi )(A);\\
{I_0} = 5\sqrt 2 (A);\\
\omega = 100\pi t(rad/s);\\
T = \frac{{2\pi }}{\omega } = 0,02(s);\\
f = \frac{1}{T} = 50(Hz);\\
\varphi = \pi (rad)
\end{array}\)
Bài 2:
Đặt điện áp xoay chiều , t tính bằng giây (s), vào hai đầu điện trở thuần R = 110 Ω.
Viết biểu thức cường độ dòng điện chạy qua điện trở thuần R.
Hướng dẫn giải :
Biên độ dòng điện xoay chiều chạy qua điện trở thuần R là :
\(\begin{array}{l}
{I_0} = \frac{{{U_0}}}{R}\\
= \frac{{220\sqrt 2 }}{{110}} = 2\sqrt 2 (A)
\end{array}\)
Dòng điện chạy qua điện trở thuần R biến đổi điều hoà cùng tần số và cùng pha với điện áp xoay chiều giữa hai đầu của nó nên biểu thức của dòng điện qua điện trở thuần R là :
\(i=2\sqrt{2}cos100\pi t(A)\)
trong đó, t tính bằng giây (s)
1. Khái niệm về dòng điện xoay chiều
-
Là dòng điện có cường độ biến thiên tuần hoàn với thời gian theo quy luật của hàm số sin hay cosin, với dạng tổng quát:
\(i=I_0cos(\omega t+\varphi )\)
-
Trong đó:
-
\(i\): giá trị của cđdđ tại thời điểm t, (cường độ tức thời).
-
\(I_0\) > 0: giá trị cực đại (cường độ cực đại).
-
\(\omega\) > 0: tần số góc (rad/s)
-
\(\omega =2\pi f=\frac{2\pi }{T}\)
-
\(f:\) tần số (Hz), T: chu kì (s)
-
\((\omega t+\varphi )\) pha của i (rad)
-
\(\varphi\) pha ban đầu (rad)
-
2. Nguyên tắc tạo ra dòng điện xoay chiều
a. Nguyên tắc:
-
Khi cho một khung dây quay đều trong từ trường đều thì trong khung dây xuất hiện suất điện động cảm ứng xoay chiều. Nếu nối hai đầu khung dây với một mạch ngoài kín thì trong mạch ngoài có dòng điện xoay chiều.
b. Khảo sát lý thuyết:
-
Xét một cuộn dây dẫn dẹt hình tròn, khép kín, quay quanh trục cố định đồng phẳng với cuộn dây đặt trong từ trường đều \(\underset{B}{\rightarrow}\) có phương vuông góc với trục quay.
-
Giả sử lúc t = 0, \(\alpha\) = 0
-
Lúc \(t> 0\rightarrow \alpha =\omega t\) , từ thông qua cuộn dây:
\(\phi =NBScos\alpha =NBScos\omega t\).
-
Vì \(\phi\) biến thiên theo thời gian t nên trong cuộn dây xuất hiện suất điện động cảm ứng:
\(e=-\frac{d\phi }{dt}=NBS\omega sin\omega t\)
-
Nếu cuộn dây kín có điện trở R thì cường độ dòng điện cảm ứng cho bởi:
3. Giá trị hiệu dụng
a. Cường độ hiệu dụng I
Cho dòng điện xoay chiều:
-
\(i=I_0cos(\omega t+\varphi )\) chạy qua điện trở R
-
Công suất tức thời tiêu thụ trong R:
\(p=Ri^2=R.I_{0}^{2}.cos^{2}(\omega t+\varphi )\)
-
Giá trị trung bình của p trong một chu kì là công suất trung bình:
\(\begin{array}{l}
P = p = RI_0^2co{s^2}\omega t\\
\Rightarrow P = p = \frac{1}{2}RI_0^2
\end{array}\)
Đặt:
-
\(I=\frac{I_0}{\sqrt{2}}\)
-
\(P=RI^2\)
-
\(I\): là giá trị hiệu dụng của cường độ dòng điện xoay chiều (cường độ hiệu dụng).
-
\(I_0\): cường độ cực đại.
Định nghĩa: Cường độ hiệu dụng của dòng điện xoay chiều là đại lượng có giá trị bằng cường độ của một dòng điện không đổi, sao cho khi đi qua cùng một điện trở R thì công suất tiêu thụ trong R bởi 2 dòng điện đó là như nhau.
b. Hiệu điện thế, suất điện động hiệu dụng
\(\begin{array}{l} U = \frac{{{U_0}}}{{\sqrt 2 }};\\ I = \frac{{{I_0}}}{{\sqrt 2 }} \end{array}\)
c. Chú ý
-
Số liệu ghi trên các thiết bị điện đều là các giá trị hiệu dụng.
-
Các thiết bị đo đối với mạch điện xoay chiều đo giá trị hiệu dụng.
Bài 1:
Xác định giá trị cực đại, tần số góc, chu kì, tần số, pha ban đầu của các dòng điện xoay chiều có cường độ tức thời cho bởi :
a. \(i=5cos(100\pi t+\frac{\pi }{4}) (A)\)
b. \(i=-5\sqrt{2}cos100\pi t (A)\)
Hướng dẫn giải :
a.
\(\begin{array}{l}
i = 5cos(100\pi t + \frac{\pi }{4})(A)\\
\to {I_0} = 5A;\\
\omega = 100\pi t(rad/s);\\
T = \frac{{2\pi }}{\omega } = 0,02(s);\\
f = \frac{1}{T} = 50(Hz);\\
\varphi = \frac{\pi }{4}(rad)
\end{array}\)
b.
\(\begin{array}{l}
i = - 5\sqrt 2 cos100\pi t(A)\\
\Leftrightarrow i = 5\sqrt 2 cos(100\pi t + \pi )(A);\\
{I_0} = 5\sqrt 2 (A);\\
\omega = 100\pi t(rad/s);\\
T = \frac{{2\pi }}{\omega } = 0,02(s);\\
f = \frac{1}{T} = 50(Hz);\\
\varphi = \pi (rad)
\end{array}\)
Bài 2:
Đặt điện áp xoay chiều , t tính bằng giây (s), vào hai đầu điện trở thuần R = 110 Ω.
Viết biểu thức cường độ dòng điện chạy qua điện trở thuần R.
Hướng dẫn giải :
Biên độ dòng điện xoay chiều chạy qua điện trở thuần R là :
\(\begin{array}{l}
{I_0} = \frac{{{U_0}}}{R}\\
= \frac{{220\sqrt 2 }}{{110}} = 2\sqrt 2 (A)
\end{array}\)
Dòng điện chạy qua điện trở thuần R biến đổi điều hoà cùng tần số và cùng pha với điện áp xoay chiều giữa hai đầu của nó nên biểu thức của dòng điện qua điện trở thuần R là :
\(i=2\sqrt{2}cos100\pi t(A)\)
trong đó, t tính bằng giây (s)