Bài 34: Kính thiên văn
Video bài giảng
1. Công dụng và cấu tạo của kính thiên văn
-
Kính thiên văn là dụng cụ quang bổ trợ cho mắt, có tác dụng tạo ảnh có góc trông lớn đối với các vật ở xa.

Hình minh họa kính thiên văn hiện đại được sử dụng cho cá nhân
-
Kính thiên văn gồm hai bộ phận chính:
-
Vật kính là thấu kính hội tụ có tiêu cự dài (và dm đến vài m).
-
Thị kính là thấu kính hội tụ có tiêu cự ngắn (vài cm).
-
-
Vật kính và thị kính đặt đồng trục, khoảng cách giữa chúng thay đổi được.
2. Sự tạo ảnh bởi kính thiên văn
-
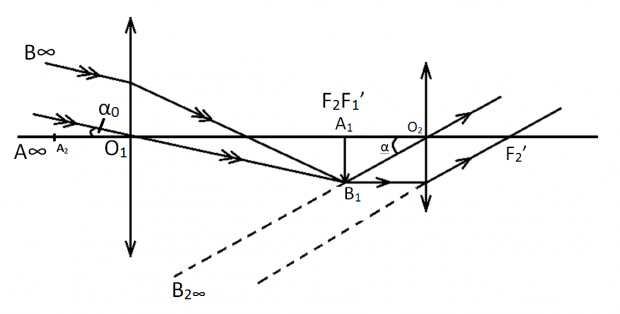
Hướng trục của kính thiên văn đến vật AB ở rất xa cần quan sát để thu ảnh thật \(A_1B_1\) trên tiêu diện ảnh của vật kính.
-
Sau đó thay đổi khoảng cách giữa vật kính và thị kính để ảnh cuối cùng \(A_2B_2\) qua thị kính là ảnh ảo, nằm trong giới hạn nhìn rỏ của mắt và góc trông ảnh phải lớn hơn năng suất phân li của mắt.
-
Mắt đặt sau thị kính để quan sát ảnh ảo này.
-
Để có thể quan sát trong một thời gian dài mà không bị mỏi mắt, ta phải đưa ảnh cuối cùng ra vô cực, gọi là ngắm chừng ở vô cực.
3. Số bội giác của kính thiên văn
Khi ngắm chừng ở vô cực:
Ta có:
\(tan\alpha _0=\frac{A_1B_1}{f_1}\);
\(tan\alpha =\frac{A_1B_1}{f_2}\)
Do đó: \(G_\propto = \frac{tan\alpha }{tan\alpha_0}=\frac{f_1}{f_2}\)
Trong đó:
-
\(G_\propto\): số bội giác khi ngắm chừng ở vô cực không phụ thuộc vị trí đặt mắt sau thị kính.
-
\(f_1\): tiêu cự của vật kính
-
\(f_2\): tiêu cự của thị kính
-
Số bội giác của kính thiên văn trong điều kiện này không phụ thuộc vị trí đặt mắt sau thị kính.
Bài 1:
Vật kính của một kính thiên văn dùng ở trường học có tiêu cự \(f_1 = 1,2 m\). Thị kính là một thấu kính hội tụ có tiêu cự \(f_2 = 4 cm\).
Tính khoảng cách giữa hai kính và số bội giác của kính thiên văn khi ngắm chừng ở vô cực.
Hướng dẫn giải:
Ta có:
Khoảng cách giữa vật kính và thị kính của kính thiên văn ngắm chừng ở vô cực:
\(O_1O_2 = f_1 + f_2 = 1,24 m.\)
Số bội giác của kính thiên văn ngắm chừng ở vô cực có biểu thức:
\(G_\infty =\frac{f_{1}}{f_{2}}=30\)
Bài 2:
Giải thích tại sao tiêu cự vật kính của kính thiên văn phải lớn.
Hướng dẫn giải:
Tiêu cự vật kính \(f_1\) của kính thiên văn phải lớn vì:
-
Số bội giác của kính thiên văn ngắm chừng ở vô cực được xác định bởi:
\(G_\propto = \frac{tan\alpha }{tan\alpha_0}=\frac{f_1}{f_2}\)
-
Để quan sát được ảnh của vật bằng kính thiên văn ta điều chỉnh thị kính để ảnh qua thị kính \(A_2B_2\) là ảnh ảo, nằm trong giới hạn thấy rõ \(C_cC_v\) của mắt, tức là ảnh \(A_1B_1\) phải nằm trong khoảng \(O_2F_2\). Vì vậy \(f_2\) phải vào khoảng cen-ti-mét.
-
Muốn G có giá trị lớn thì ta phải tăng giá trị của \(f_1\) => Tiêu cự vật kính của kính thiên văn phải lớn
1. Công dụng và cấu tạo của kính thiên văn
-
Kính thiên văn là dụng cụ quang bổ trợ cho mắt, có tác dụng tạo ảnh có góc trông lớn đối với các vật ở xa.

Hình minh họa kính thiên văn hiện đại được sử dụng cho cá nhân
-
Kính thiên văn gồm hai bộ phận chính:
-
Vật kính là thấu kính hội tụ có tiêu cự dài (và dm đến vài m).
-
Thị kính là thấu kính hội tụ có tiêu cự ngắn (vài cm).
-
-
Vật kính và thị kính đặt đồng trục, khoảng cách giữa chúng thay đổi được.
2. Sự tạo ảnh bởi kính thiên văn

-
Hướng trục của kính thiên văn đến vật AB ở rất xa cần quan sát để thu ảnh thật \(A_1B_1\) trên tiêu diện ảnh của vật kính.
-
Sau đó thay đổi khoảng cách giữa vật kính và thị kính để ảnh cuối cùng \(A_2B_2\) qua thị kính là ảnh ảo, nằm trong giới hạn nhìn rỏ của mắt và góc trông ảnh phải lớn hơn năng suất phân li của mắt.
-
Mắt đặt sau thị kính để quan sát ảnh ảo này.
-
Để có thể quan sát trong một thời gian dài mà không bị mỏi mắt, ta phải đưa ảnh cuối cùng ra vô cực, gọi là ngắm chừng ở vô cực.
3. Số bội giác của kính thiên văn
Khi ngắm chừng ở vô cực:
Ta có:
\(tan\alpha _0=\frac{A_1B_1}{f_1}\);
\(tan\alpha =\frac{A_1B_1}{f_2}\)
Do đó: \(G_\propto = \frac{tan\alpha }{tan\alpha_0}=\frac{f_1}{f_2}\)
Trong đó:
-
\(G_\propto\): số bội giác khi ngắm chừng ở vô cực không phụ thuộc vị trí đặt mắt sau thị kính.
-
\(f_1\): tiêu cự của vật kính
-
\(f_2\): tiêu cự của thị kính
-
Số bội giác của kính thiên văn trong điều kiện này không phụ thuộc vị trí đặt mắt sau thị kính.
Bài 1:
Vật kính của một kính thiên văn dùng ở trường học có tiêu cự \(f_1 = 1,2 m\). Thị kính là một thấu kính hội tụ có tiêu cự \(f_2 = 4 cm\).
Tính khoảng cách giữa hai kính và số bội giác của kính thiên văn khi ngắm chừng ở vô cực.
Hướng dẫn giải:
Ta có:
Khoảng cách giữa vật kính và thị kính của kính thiên văn ngắm chừng ở vô cực:
\(O_1O_2 = f_1 + f_2 = 1,24 m.\)
Số bội giác của kính thiên văn ngắm chừng ở vô cực có biểu thức:
\(G_\infty =\frac{f_{1}}{f_{2}}=30\)
Bài 2:
Giải thích tại sao tiêu cự vật kính của kính thiên văn phải lớn.
Hướng dẫn giải:
Tiêu cự vật kính \(f_1\) của kính thiên văn phải lớn vì:
-
Số bội giác của kính thiên văn ngắm chừng ở vô cực được xác định bởi:
\(G_\propto = \frac{tan\alpha }{tan\alpha_0}=\frac{f_1}{f_2}\)
-
Để quan sát được ảnh của vật bằng kính thiên văn ta điều chỉnh thị kính để ảnh qua thị kính \(A_2B_2\) là ảnh ảo, nằm trong giới hạn thấy rõ \(C_cC_v\) của mắt, tức là ảnh \(A_1B_1\) phải nằm trong khoảng \(O_2F_2\). Vì vậy \(f_2\) phải vào khoảng cen-ti-mét.
-
Muốn G có giá trị lớn thì ta phải tăng giá trị của \(f_1\) => Tiêu cự vật kính của kính thiên văn phải lớn