Bài 33: Kính hiển vi
Video bài giảng
1. Công dụng và cấu tạo của kính hiển vi
-
Kính hiển vi là dụng cụ quang học bỗ trợ cho mắt để nhìn các vật rất nhỏ, bằng cách tạo ra ảnh có góc trông lớn. Số bội giác của kính hiển vi lớn hơn nhiều so với số bội giác của kính lúp.
-
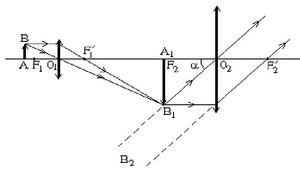
Kính hiển vi gồm vật kính là thấu kính hội tụ có tiêu rất nhỏ (vài mm) và thị kính là thấu kính hội tụ có tiêu cự nhỏ (vài cm). Vật kính và thị kính đặt đồng truc, khoảng cách giữa chúng \(O_1O_2=l\) không đổi. Khoảng cách \(F_1'F_2'=\delta\) gọi là độ dài quang học của kính.
-
Ngoài ra còn có bộ phận tụ sáng để chiếu sáng vật cần quan sát. Đó thường là một gương cầu lỏm.
-
Hình ảnh một số sinh vật chụp được khi quan sát qua kính hiển vi
Hình ảnh lưỡi xanh của một con dế, phóng đại lên 25 lần.
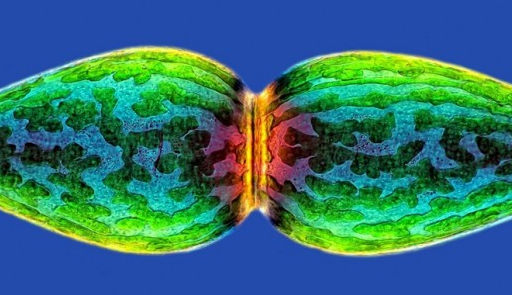
Hình ảnh của một loại vi tảo nhỏ, phóng đại 40 lần.
2. Sự tạo ảnh bởi kính hiển vi
Sơ đồ tạo ảnh :
-
\(A_1B_1\) là ảnh thật lớn hơn nhiều so với vật AB. \(A_2B_2\) là ảnh ảo lớn hơn nhiều so với ảnh trung gian \(A_1B_1\).
-
Mắt đặt sau thị kính để quan sát ảnh ảo \(A_2B_2\) .
-
Điều chỉnh khoảng cách từ vật đến vật kính (\(d_1\)) sao cho ảnh cuối cùng (\(A_2B_2\) ) hiện ra trong giới hạn nhìn rỏ của mắt và góc trông ảnh phải lớn hơn hoặc bằng năng suất phân li của mắt.
-
Nếu ảnh sau cùng \(A_2B_2\) của vật quan sát được tạo ra ở vô cực thì ta có sự ngắm chừng ở vô cực.
-
Khi quan sát vật bằng kính hiển vi phải thực hiện như sau
-
Vật phải được kẹp giữa hai tấm thủy tinh mỏng trong suốt, đó là tiêu bản
-
Vật được cố định trên giá, ta dời toàn bộ ống kính từ vị trí sát vật ra xa dần bằng ốc vi cấp.
-
3. Số bội giác của kính hiển vi
Khi ngắm chừng ở cực cận:
-
\(G_c=\left |\frac{d_1'd_2'}{d_1d_2} \right |\)
Khi ngắm chừng ở vô cực:
-
\(G_\propto =\left |k_1 \right |.G_2=\frac{\delta .OC_c}{f_1f_2}\)
-
Với \(\delta =O_1O_2-f_1-f_2\)
Trong đó:
-
\(G_\propto\): số bội giác của kính hiển vi khi ngắm chừng ở vô cực
-
\(k_1\): số phóng đại của vật kính L1
-
\(G_2\): số bộ giác của thị kính L2
-
\(\delta\): độ dài quang học
-
\(f_1\): tiêu cự của vật kính L1
-
\(f_2\): tiêu cự của thị kính L2
-
Đ \(=OC_c\): khoảng nhìn rõ gần nhất của mắt
Bài 1:
Một kính hiển vi có các tiêu cự vật kính và thị kính là \(f_1 = 1 cm, f_2 = 4 cm\). Độ dài quang học của kính là 16 cm. Người quan sát có mắt không bị tật và có khoảng cực cận \(OC_c = 20 cm\). Người này ngắm chừng ở vô cực. Tính số bội giác của ảnh.
Hướng dẫn giải:
Ta có:
Sơ đồ tạo ảnh:
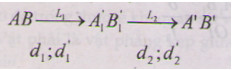
Số bội giác của ảnh ngắm chừng ở vô cực tính theo công thức:
\(G_{\infty } = \frac{\delta D}{f_1.f_2} = 80.\)
Bài 2:
Muốn điều chỉnh kính hiển vi, ta thực hiện ra sao? Khoảng xê dịch điều chỉnh kính hiển vi có giá trị như thế nào ?
Hướng dẫn giải:
Cách điều chỉnh kính hiển vi:
-
Vật phẳng cần quan sát kẹp giữa hai tấm thủy tinh mỏn trong suốt (gọi là tiêu bản )
-
Đặt vật cố định trên giá đồng thời di chuyển toàn bộ ống kính (cả vật kính và thị kính) từ vị trí sát nhập ra xa dần bằng ốc vít vị cấp.
-
Điều chỉnh khoảng cách từ vật đến kính \(d_1\) sao cho ảnh của bật qua kính nằm trong khoảng giới hạn thấy rõ \(C_cC_v\) của mắt.
Đối với kính hiển vi, khoảng dịch chuyển \(\Delta d_1\) này rất nhỏ (cỡ chừng vài chục μm).
1. Công dụng và cấu tạo của kính hiển vi
-
Kính hiển vi là dụng cụ quang học bỗ trợ cho mắt để nhìn các vật rất nhỏ, bằng cách tạo ra ảnh có góc trông lớn. Số bội giác của kính hiển vi lớn hơn nhiều so với số bội giác của kính lúp.

-
Kính hiển vi gồm vật kính là thấu kính hội tụ có tiêu rất nhỏ (vài mm) và thị kính là thấu kính hội tụ có tiêu cự nhỏ (vài cm). Vật kính và thị kính đặt đồng truc, khoảng cách giữa chúng \(O_1O_2=l\) không đổi. Khoảng cách \(F_1'F_2'=\delta\) gọi là độ dài quang học của kính.
-
Ngoài ra còn có bộ phận tụ sáng để chiếu sáng vật cần quan sát. Đó thường là một gương cầu lỏm.
-
Hình ảnh một số sinh vật chụp được khi quan sát qua kính hiển vi
Hình ảnh lưỡi xanh của một con dế, phóng đại lên 25 lần.
Hình ảnh của một loại vi tảo nhỏ, phóng đại 40 lần.
2. Sự tạo ảnh bởi kính hiển vi
Sơ đồ tạo ảnh :
-
\(A_1B_1\) là ảnh thật lớn hơn nhiều so với vật AB. \(A_2B_2\) là ảnh ảo lớn hơn nhiều so với ảnh trung gian \(A_1B_1\).
-
Mắt đặt sau thị kính để quan sát ảnh ảo \(A_2B_2\) .
-
Điều chỉnh khoảng cách từ vật đến vật kính (\(d_1\)) sao cho ảnh cuối cùng (\(A_2B_2\) ) hiện ra trong giới hạn nhìn rỏ của mắt và góc trông ảnh phải lớn hơn hoặc bằng năng suất phân li của mắt.
-
Nếu ảnh sau cùng \(A_2B_2\) của vật quan sát được tạo ra ở vô cực thì ta có sự ngắm chừng ở vô cực.
-
Khi quan sát vật bằng kính hiển vi phải thực hiện như sau
-
Vật phải được kẹp giữa hai tấm thủy tinh mỏng trong suốt, đó là tiêu bản
-
Vật được cố định trên giá, ta dời toàn bộ ống kính từ vị trí sát vật ra xa dần bằng ốc vi cấp.
-
3. Số bội giác của kính hiển vi
Khi ngắm chừng ở cực cận:
-
\(G_c=\left |\frac{d_1'd_2'}{d_1d_2} \right |\)
Khi ngắm chừng ở vô cực:
-
\(G_\propto =\left |k_1 \right |.G_2=\frac{\delta .OC_c}{f_1f_2}\)
-
Với \(\delta =O_1O_2-f_1-f_2\)
Trong đó:
-
\(G_\propto\): số bội giác của kính hiển vi khi ngắm chừng ở vô cực
-
\(k_1\): số phóng đại của vật kính L1
-
\(G_2\): số bộ giác của thị kính L2
-
\(\delta\): độ dài quang học
-
\(f_1\): tiêu cự của vật kính L1
-
\(f_2\): tiêu cự của thị kính L2
-
Đ \(=OC_c\): khoảng nhìn rõ gần nhất của mắt
Bài 1:
Một kính hiển vi có các tiêu cự vật kính và thị kính là \(f_1 = 1 cm, f_2 = 4 cm\). Độ dài quang học của kính là 16 cm. Người quan sát có mắt không bị tật và có khoảng cực cận \(OC_c = 20 cm\). Người này ngắm chừng ở vô cực. Tính số bội giác của ảnh.
Hướng dẫn giải:
Ta có:
Sơ đồ tạo ảnh:
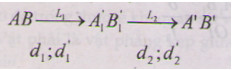
Số bội giác của ảnh ngắm chừng ở vô cực tính theo công thức:
\(G_{\infty } = \frac{\delta D}{f_1.f_2} = 80.\)
Bài 2:
Muốn điều chỉnh kính hiển vi, ta thực hiện ra sao? Khoảng xê dịch điều chỉnh kính hiển vi có giá trị như thế nào ?
Hướng dẫn giải:
Cách điều chỉnh kính hiển vi:
-
Vật phẳng cần quan sát kẹp giữa hai tấm thủy tinh mỏn trong suốt (gọi là tiêu bản )
-
Đặt vật cố định trên giá đồng thời di chuyển toàn bộ ống kính (cả vật kính và thị kính) từ vị trí sát nhập ra xa dần bằng ốc vít vị cấp.
-
Điều chỉnh khoảng cách từ vật đến kính \(d_1\) sao cho ảnh của bật qua kính nằm trong khoảng giới hạn thấy rõ \(C_cC_v\) của mắt.
Đối với kính hiển vi, khoảng dịch chuyển \(\Delta d_1\) này rất nhỏ (cỡ chừng vài chục μm).
.PNG)