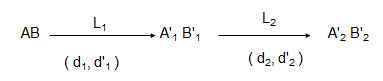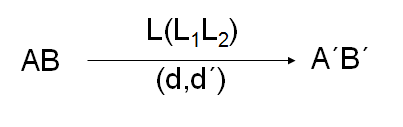Bài 30: Giải bài toán về hệ thấu kính
Video bài giảng
1. Lập sơ đồ tạo ảnh
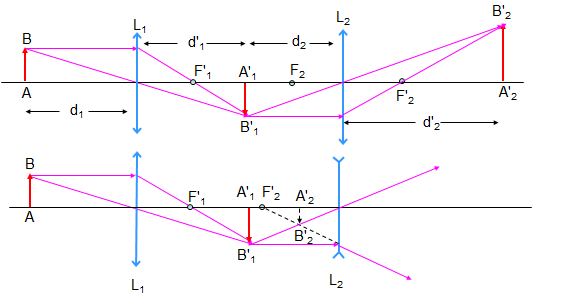
1.1. Hệ hai thấu kính đồng trục ghép cách nhau:
Sơ đồ tạo ảnh
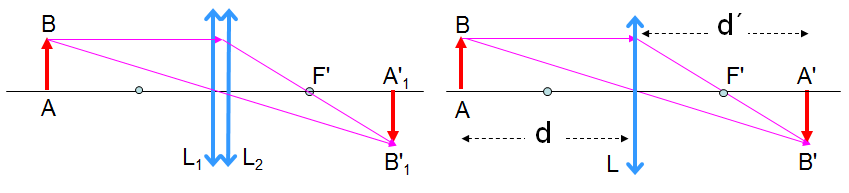
1.2. Hệ hai thấu kính đồng trục ghép sát nhau:
Hệ hai thấu kính \(L_1\) và \(L_2\) có tiêu cự \(f_1\) và \(f_2\) tương đương với một thấu kính L có tiêu cự f:
\(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
hay: \(D=D_1+D_2\)
Vật AB qua hệ cho ảnh như qua thấu kính L:
2. Thực hiện tính toán
Gọi \(l\) là khoảng cách từ thấu kính \(L_1\) đến thấu kính \(L_2\)
-
Khoảng cách từ ảnh \(A_1'B_1'\)đến thấu kính \(L_1\):
\(d_1'=\frac{d_1f_1}{d_1-f_1}\)
-
Khoảng cách từ \(A_1'B_1'\) (xem như là vật) đến thấu kính \(L_2\) : \(d_2=l-d_1'\)
-
Khoảng cách từ ảnh \(A_2'B_2'\) đến thấu kính \(L_2\):
\(d_2'=\frac{d_2f_2}{d_2-f_2}\)
-
Số phóng đại ảnh sau cùng:
\(\begin{array}{l}
k = \frac{{{A_{2'}}{B_{2'}}}}{{AB}} = \frac{{{A_{2'}}{B_{2'}}}}{{{A_{1'}}{B_{1'}}}}\frac{{{A_{1'}}{B_{1'}}}}{{AB}}\\
\Rightarrow k = {k_1}.{k_2} = \frac{{{d_{1'}}{d_{2'}}}}{{{d_1}{d_2}}}
\end{array}\)
Bài 1:
Hai thấu kính, một hội tụ \((f_1 = 20 cm)\), một phân kỳ \((f_2 = -10 cm)\), có cùng trục chính. Khoảng cách hai quang tâm là l = 30 cm. Vật AB vuông góc với trục chính được đặt bên trái \(L_1\) và cách \(L_1\) một đoạn \(d_1\).
a) Cho \(d_1= 20 cm\), hãy xác định vị trí và tính số phóng đại ảnh cuối cùng cho bởi hệ hai thấu kính. Vẽ ảnh.
b) Tính \(d_1\) để ảnh sau cùng là ảnh ảo và bằng hai lần vật.
Hướng dẫn giải:
a.
Sơ đồ tạo ảnh qua hệ thấu kính:
Ta có: \(d_1=20cm, f_1=20cm, l=30cm\)
⇒ \(d_1'=\propto\)
\(d_2=l-d_1'=-\propto\)
⇒ \(d_2'=f_2=-10cm\)
Vẽ hình:
Từ hình vẽ ta thấy:
-
Vì \(A_1B_1\) ở vô cực nên chùm tia sáng từ AB tới qua tâm O1 sẽ qua \(A_1B_1\) và là chùm tia song song .
-
Tương tự, chùm tia sáng từ \(A_1B_1\) tới qua tâm O2 sẽ qua \(A_2B_2\) cùng là chùm tia song song.
⇒ Tam giác \(ABO_1\)đồng dạng với tam giác \(A_2B_2O_2\) suy ra:
\(\begin{array}{l}
k = \frac{{{A_2}{B_2}}}{{AB}} = \frac{{{A_2}{O_2}}}{{A{O_1}}}\\
= \frac{{\left| {{{d'}_2}} \right|}}{{{d_1}}} = \frac{{\left| { - 10} \right|}}{{20}} = \frac{1}{2}
\end{array}\)
b.
-
Ảnh \(A_2B_2\) là ảnh ảo và bằng hai lần vật. Ta có:
\(\Rightarrow d'_1=\frac{d_1.f_1}{d_1-f_1}=20.\frac{d_1}{d_1-20}\)
\(d_2=1-d_1\Rightarrow d_2=30\)
\(=20.\frac{d_1}{d_1-20}=\frac{10(d_1-60)}{d_1-20}\)
\(\Rightarrow \frac{5(60-d_1)}{d_1-40}< 0\)
\(\Rightarrow d_1<40 \ cm\) và \(d_2>60 \ cm\)
-
Ảnh \(A_2B_2\) là ảnh ảo và bằng hai lần vật AB:
\(\begin{array}{l}
k = \left( { - \frac{{{d_1}}}{{{d_1}}}} \right).\left( { - \frac{{{d_2}}}{{{d_2}}}} \right) = \frac{{{d_1}.{d_2}}}{{{d_1}.{d_2}}}\\
= \frac{{10}}{{{d_1} - 40}} = \pm 2\\
\Rightarrow k = \pm 2 = \frac{{20}}{{{d_1} - 60}}\left( * \right)
\end{array}\)
-
Giải phương trình (*) ra ta được: \(d_1\)=35cm ( nhận) và \(d_1\) =45cm (loại)
Đáp số:
a. \(d_2'=f_2=-10cm\) và \(k=\frac{1}{2}\)
b. \(d_1\)=35cm
1. Lập sơ đồ tạo ảnh
1.1. Hệ hai thấu kính đồng trục ghép cách nhau:
Sơ đồ tạo ảnh
1.2. Hệ hai thấu kính đồng trục ghép sát nhau:
Hệ hai thấu kính \(L_1\) và \(L_2\) có tiêu cự \(f_1\) và \(f_2\) tương đương với một thấu kính L có tiêu cự f:
\(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
hay: \(D=D_1+D_2\)
Vật AB qua hệ cho ảnh như qua thấu kính L:
2. Thực hiện tính toán
Gọi \(l\) là khoảng cách từ thấu kính \(L_1\) đến thấu kính \(L_2\)
-
Khoảng cách từ ảnh \(A_1'B_1'\)đến thấu kính \(L_1\):
\(d_1'=\frac{d_1f_1}{d_1-f_1}\)
-
Khoảng cách từ \(A_1'B_1'\) (xem như là vật) đến thấu kính \(L_2\) : \(d_2=l-d_1'\)
-
Khoảng cách từ ảnh \(A_2'B_2'\) đến thấu kính \(L_2\):
\(d_2'=\frac{d_2f_2}{d_2-f_2}\)
-
Số phóng đại ảnh sau cùng:
\(\begin{array}{l}
k = \frac{{{A_{2'}}{B_{2'}}}}{{AB}} = \frac{{{A_{2'}}{B_{2'}}}}{{{A_{1'}}{B_{1'}}}}\frac{{{A_{1'}}{B_{1'}}}}{{AB}}\\
\Rightarrow k = {k_1}.{k_2} = \frac{{{d_{1'}}{d_{2'}}}}{{{d_1}{d_2}}}
\end{array}\)
Bài 1:
Hai thấu kính, một hội tụ \((f_1 = 20 cm)\), một phân kỳ \((f_2 = -10 cm)\), có cùng trục chính. Khoảng cách hai quang tâm là l = 30 cm. Vật AB vuông góc với trục chính được đặt bên trái \(L_1\) và cách \(L_1\) một đoạn \(d_1\).
a) Cho \(d_1= 20 cm\), hãy xác định vị trí và tính số phóng đại ảnh cuối cùng cho bởi hệ hai thấu kính. Vẽ ảnh.
b) Tính \(d_1\) để ảnh sau cùng là ảnh ảo và bằng hai lần vật.
Hướng dẫn giải:
a.
Sơ đồ tạo ảnh qua hệ thấu kính:
Ta có: \(d_1=20cm, f_1=20cm, l=30cm\)
⇒ \(d_1'=\propto\)
\(d_2=l-d_1'=-\propto\)
⇒ \(d_2'=f_2=-10cm\)
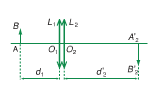
Vẽ hình:
Từ hình vẽ ta thấy:
-
Vì \(A_1B_1\) ở vô cực nên chùm tia sáng từ AB tới qua tâm O1 sẽ qua \(A_1B_1\) và là chùm tia song song .
-
Tương tự, chùm tia sáng từ \(A_1B_1\) tới qua tâm O2 sẽ qua \(A_2B_2\) cùng là chùm tia song song.
⇒ Tam giác \(ABO_1\)đồng dạng với tam giác \(A_2B_2O_2\) suy ra:
\(\begin{array}{l}
k = \frac{{{A_2}{B_2}}}{{AB}} = \frac{{{A_2}{O_2}}}{{A{O_1}}}\\
= \frac{{\left| {{{d'}_2}} \right|}}{{{d_1}}} = \frac{{\left| { - 10} \right|}}{{20}} = \frac{1}{2}
\end{array}\)
b.
-
Ảnh \(A_2B_2\) là ảnh ảo và bằng hai lần vật. Ta có:
\(\Rightarrow d'_1=\frac{d_1.f_1}{d_1-f_1}=20.\frac{d_1}{d_1-20}\)
\(d_2=1-d_1\Rightarrow d_2=30\)
\(=20.\frac{d_1}{d_1-20}=\frac{10(d_1-60)}{d_1-20}\)
\(\Rightarrow \frac{5(60-d_1)}{d_1-40}< 0\)
\(\Rightarrow d_1<40 \ cm\) và \(d_2>60 \ cm\)
-
Ảnh \(A_2B_2\) là ảnh ảo và bằng hai lần vật AB:
\(\begin{array}{l}
k = \left( { - \frac{{{d_1}}}{{{d_1}}}} \right).\left( { - \frac{{{d_2}}}{{{d_2}}}} \right) = \frac{{{d_1}.{d_2}}}{{{d_1}.{d_2}}}\\
= \frac{{10}}{{{d_1} - 40}} = \pm 2\\
\Rightarrow k = \pm 2 = \frac{{20}}{{{d_1} - 60}}\left( * \right)
\end{array}\)
-
Giải phương trình (*) ra ta được: \(d_1\)=35cm ( nhận) và \(d_1\) =45cm (loại)
Đáp số:
a. \(d_2'=f_2=-10cm\) và \(k=\frac{1}{2}\)
b. \(d_1\)=35cm