Phương pháp giải hệ phương trình ôn thi đại học
Hệ phương trình là bài toán thường gặp trong đề thi tốt nghiệp cũng như đề thi đại học. Nhằm giúp các bạn học sinh làm tốt những bài toán dạng này, Tìm Đáp Án xin giới thiệu tới các bạn "Phương pháp giải hệ phương trình thường gặp trong đề thi đại học". Tài liệu này giúp các bạn tiếp cận với bài hệ phương trình trong những năm gần đây bằng nhiều phương pháp khác nhau.
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc
Tuyển tập 100 hệ phương trình luyện thi đại học
260 bài toán phương trình và hệ phương trình trong ôn thi đại học
Ôn thi Đại học môn Toán - Chuyên đề: Tổ hợp và xác suất
Ôn thi Đại học môn Toán - Chuyên đề: Hình học giải tích trong không gian Oxyz
MỘT SỐ PHƯƠNG PHÁP GIẢI HỆ PHƯƠNG TRÌNH
1. Phương pháp thế
Nội dung phương pháp: Thông thường ta rút một biến hoặc một biểu thức thích hợp từ một phương trình và thay vào phương trình còn lại của hệ ta thu được phương trình một ẩn.
Chú ý:
- Phương trình một ẩn này phải giải được
- Một phương trình trong hệ có thể đưa về tích của các phương trình bậc nhất hai ẩn
| Ví dụ 1: Giải hệ phương trình { | x4 + 2x3y + x2y2 = 2x + 9 (1) |
Giải
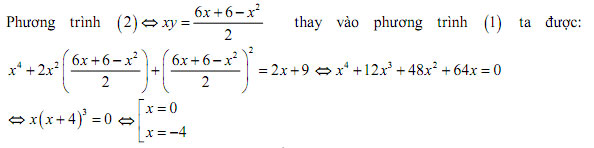
Với x = 0 thay vào phương trình (2) ta thấy không thỏa mãn.
Với x = -4 thay vào phương trình (2) ta được y = 17/4.
Vậy nghiệm của hệ phương trình là: x = -4 và y = 17/4.
Bài tập
Giải các hệ phương trình sau

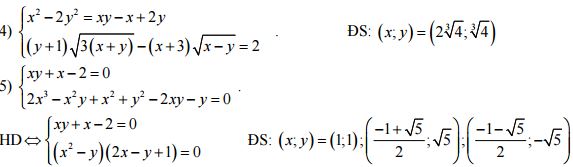
2. Phương pháp đặt ẩn phụ
Nội dung phương pháp: Điểm quan trọng nhất trong việc giải hệ là phát hiện ẩn phụ u = f(x; y), v = g(x; y). Có ngay trong từng phương trình hoặc xuất hiện sau một số phép biến đổi cơ bản
Ví dụ 1: Giải hệ phương trình: 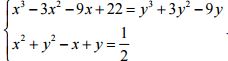
Giải:
Đặt y = -z, ta được hệ phương trình:
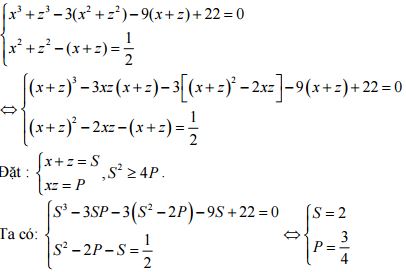
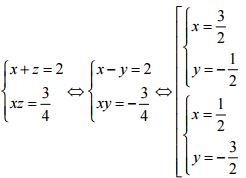
Vậy nghiệm của hệ phương trình là: x = 3/2 và y = -1/2; x = 1/2 và y = -3/2.
Bài tập
Giải các hệ phương trình sau: