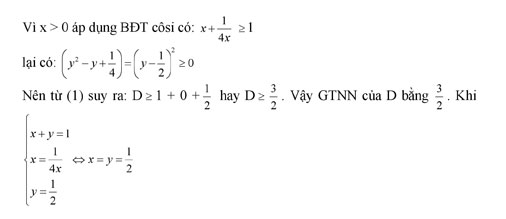Đề thi thử vào lớp 10 THPT môn Toán
Đề thi thử vào lớp 10 THPT môn Toán trường THCS Minh Nghĩa, Thanh Hóa năm 2016 - 2017 được TimDapAnsưu tầm và đăng tải nhằm giúp các em học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các em cùng tham khảo.
Bộ đề thi vào lớp 10 THPT môn Toán năm học 2016 - 2017
Đề thi thử vào lớp 10 THPT môn Ngữ văn phòng GD&ĐT Tây Hồ, Hà Nội năm 2016 - 2017
| TRƯỜNG THCS MINH NGHĨA |
KỲ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2016 – 2017 Môn thi: Toán (Thời gian làm bài: 120 phút, không kể thời gian phát đề) |
Bài 1: (2 điểm)
1- Giải các phương trình sau:
a) x - 1 = 0
b) x2 - 3x + 2 = 0
2- Giải hệ phương trình: 
3, Viết phương trình đường thẳng đi qua A(1; 2) và song song với đường thẳng y = 3x + 5
Bài 2 (2 điểm):
Cho biểu thức 
1. Rút gọn biểu thức A.
2. Tính giá trị của A tại a = 6 + 4√2
Bài 3: (2 điểm)
Trong mặt phẳng toạ độ Oxy cho Parabol (P) có phương trình: y = x2 và đường thẳng (d) có phương trình: y = 2mx – 2m + 3 (m là tham số)
a) Tìm toạ độ các điểm thuộc (P) biết tung độ của chúng bằng 2
b) Chứng minh rằng (P) và (d) cắt nhau tại hai điểm phân biệt với mọi m.
Gọi là các tung độ giao điểm của (P) và (d), tìm m để
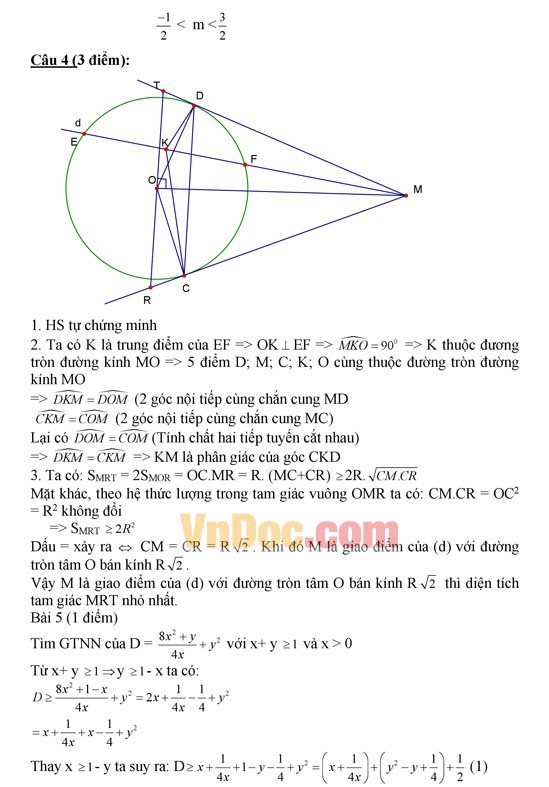
Bài 4 (3 điểm): Cho đường tròn tâm O bán kính R và đường thẳng (d) không đi qua O, cắt đường tròn (O) tại 2 điểm E, F. Lấy điểm M bất kì trên tia đối FE, qua M kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là các tiếp điểm).
1. Chứng minh tứ giác MCOD nội tiếp trong một đường tròn.
2. Gọi K là trung điểm của đoạn thẳng EF. Chứng minh KM là phân giác của góc CKD.
3. Đường thẳng đi qua O và vuông góc với MO cắt các tia MC, MD theo thứ tự tại R, T. Tìm vị trí của điểm M trên (d) sao cho diện tích tam giác MRT nhỏ nhất.
Bài 5: (1 điểm)
Tìm giá trị nhỏ nhất của biểu thức 
Đáp án đề thi thử vào lớp 10 THPT môn Toán
Bộ đề thi vào lớp 10 THPT môn Ngữ văn năm học 2016 - 2017
Đề thi thử vào lớp 10 THPT môn Toán phòng GD&ĐT Vũ Thư, Thái Bình năm 2015 - 2016
Bài 1:
1, mỗi y cho 0,5đ
a, x = 1
b, x1 = 1; x2 = 2
2, 3 mối ý cho 0,5đ
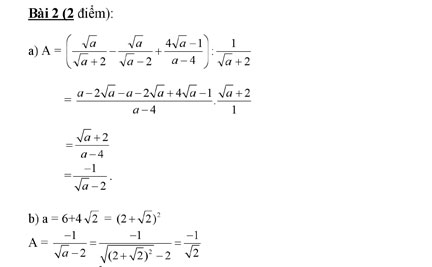
Bài 3:
1. A (√2; 2) và B (-√2; 2)
2, Viết pt hoành độ giao điểm: x2 = 2mx – 2m + 3
<=> x2-2mx +2m – 3=0
Ta có: ∆'= m2 - 2m + 3 = (m-1)2+2 > 0 với mọi m suy ra (P) và đường thẳng d cắt nhau tại 2 điểm phân biệt với mọi m
Áp dụng viét ta có: x1+x2 = 2m
<=> x1x2 = 2m – 3
Theo bài ra ta có: (x1+x2)2-2 x1x2 < 9
<=>4m2 - 2(2m – 3) < 9
<=> 4m2 - 4m - 3 < 0
