Đề thi thử THPT Quốc gia môn Toán năm 2016

Kỳ thi THPT Quốc gia 2016 đang tới gần. Nhằm giúp các bạn thí sinh gấp rút luyện thi, thử sức trước kỳ thi quan trọng này, Tìm Đáp Án xin giới thiệu Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Ân Thi, Hưng Yên (Lần 3) có đáp án đi kèm. Mời các bạn cùng tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 3)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 2)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Gia Lộc, Hải Dương (Lần 1)

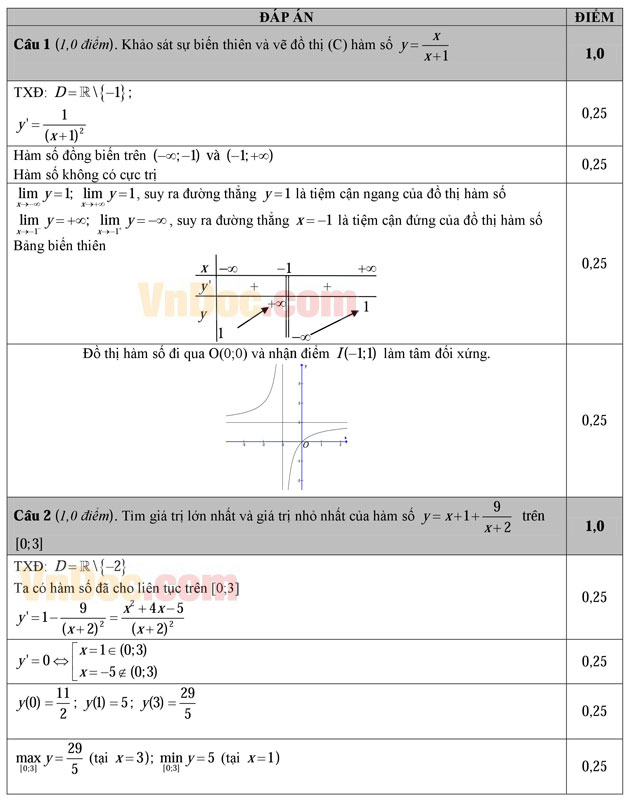
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số .

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0; 3]

Câu 3 (1,0 điểm).

a) Cho số phức z thỏa mãn 2z = 5i + iz, tính

b) Giải phương trình log₂x.log₂(2x) − 2 = 0

Câu 4 (1,0 điểm). Tính tích phân sau: .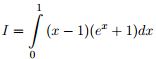

Câu 5 (1,0 điểm). Trong hệ tọa độ Oxyz, cho điểm I(2; −5; 6) và mặt phẳng (P) có phương trình x − 2y + 2z + 3 = 0. Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P)? Tìm tọa độ tiếp điểm của mặt cầu (S) và mặt phẳng (P)?

Câu 6 (1,0 điểm).

a) Giải phương trình: cos 2x − sin x + 2 = 0

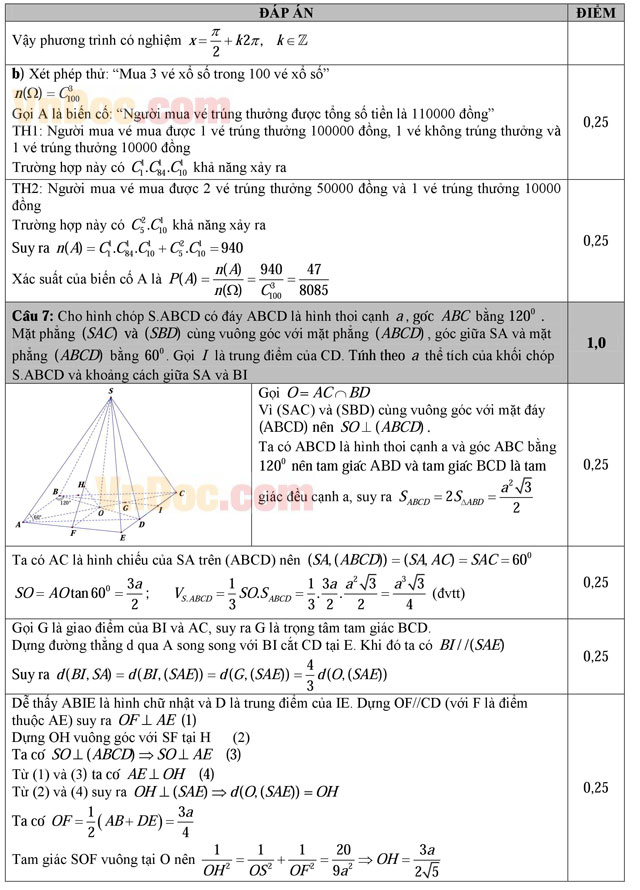
b) Có 100 vé xổ số, trong đó chỉ có 1 vé trúng thưởng 100000 đồng, 5 vé trúng thưởng 50000 đồng, 10 vé trúng thưởng 10000 đồng, còn các vé khác không trúng thưởng. Một người mua 3 vé xổ số, tính xác suất để người đó trúng thưởng và có tổng số tiền thưởng là 110000 đồng?

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC bằng 120⁰. Mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD), góc giữa SA và mặt phẳng (ABCD) bằng 60⁰. Gọi I là trung điểm của CD. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa SA và BI?

Câu 8 (1,0 điểm). Giải phương trình sau:

Câu 9 (1,0 điểm). Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD, gọi M là trung điểm của AD, đường thẳng qua M vuông góc với MB cắt CD tại E, gọi H là hình chiếu của M trên BE, gọi K là giao điểm của BD và AE. Tìm tọa độ các đỉnh của hình chữ nhật ABCD biết ME: x − 3 = 0, H(−1; 2) và K(-1/5; 2/5).

Câu 10 (1,0 điểm). Cho a, b, c là ba số dương thỏa mãn: a + b + c = 3. Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016