ĐỀ THI MÔN: TOÁN (BẢNG A)

Bài 1. (4,5 điểm)

a) Chứng minh đẳng thức:

b) Giải hệ phương trình:

Bài 2. (3,5 điểm)

Cho hàm số bậc nhất y = mx + m - 1 (*) (với m là tham số).

a) Tìm các giá trị của m để đồ thị của hàm số (*) tạo với các trục tọa độ Oxy một tam giác có diện tích bằng 2.

b) Chứng minh rằng đồ thị của hàm số (*) luôn đi qua một điểm cố định với mọi giá trị của m.

Bài 3. (4,0 điểm)

Cho x, y, z là ba số thực dương thoả mãn xyz = 1. Tìm giá trị lớn nhất của biểu thức:

Bài 4. (6,0 điểm)

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Gọi I là một điểm trên cung nhỏ AB (I không trùng với A và B). Gọi M,N, P theo thứ tự là hình chiếu của điểm I trên các đường thẳng BC, AC, AB.

a) Chứng minh rằng ba điểm M, N, P thẳng hàng.

b) Xác định vị trí của điểm I để đoạn thẳng MN có độ dài lớn nhất.

Bài 5. (2,0 điểm)

Giải phương trình sau:

ĐỀ THI MÔN: TOÁN (BẢNG B)

Câu 1. (4,0 điểm)

Cho biểu thức

a) Rút gọn biểu thức P.

b) Tìm x nguyên để P nhận giá trị nguyên.

Câu 2. (4,0 điểm)

Cho ba số thực a, b, c thỏa mãn đồng thời: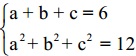

Tính giá trị của biểu thức P = (a - 3)²⁰¹³ + (b - 3)²⁰¹³ + (c - 3)²⁰¹³.

Câu 3. (4,0 điểm)

Giải phương trình:

Câu 4. (6,0 điểm)

Cho đường tròn (O) và BC là một dây cung không đi qua tâm O. Điểm A bất kì nằm trên cung lớn BC của đường tròn (O) sao cho điểm O luôn nằm trong tam giác ABC (A ≠ B; C). Các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh tứ giác BFEC nội tiếp.

b) Đường cao AD cắt đường tròn (O) tại I. Chứng minh I đối xứng với H qua BC.

c) Gọi M là trung điểm của BC. Chứng minh AH = 2OM.

Câu 5. (2,0 điểm)

Cho ba số thực dương x, y, z thỏa mãn

Tìm giá trị lớn nhất của biểu thức P = xyz.