Bộ đề thi thử vào lớp 10 môn Toán

Bộ đề thi thử vào lớp 10 môn Toán năm học 2017 - 2018 tổng hợp nhiều đề thử vào lớp 10 của tất cả các trường trên cả nước, nội dung đề thi bám sát chương trình học theo yêu cầu và quy định của Bộ GD&ĐT. Mời các em tham khảo để làm quen với cấu trúc đề thi, các dạng bài tập, mỗi đề thi kèm theo đáp án và hướng dẫn giải chi tiết giúp các em dễ dàng hơn trong việc ôn tập cũng như rèn luyện kỹ năng giải đề.

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Yên Sơn, Tuyên Quang năm học 2017 - 2018

2 Đề thi thử vào lớp 10 môn Toán có đáp án

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Sơn Dương, Tuyên Quang năm học 2017 - 2018

ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
Năm học: 2017 - 2018
Môn: Toán
Thời gian làm bài: 90 phút

MÃ ĐỀ 01

Câu 1.

a) Tìm điều kiện của x để biểu thức sau có nghĩa: A=√x+1 +√3-2x

b) Rút gọn biểu thức: B= 3√8-√50-√(1-√2)²

c) Cho đường thẳng (d): y = 2x + m - 1. Tìm m để đường thẳng (d) cắt các trục tọa độ Ox, Oy lần lượt tại M và N sao cho ΔMON có diện tích bằng 1

Câu 2. Cho biểu thức

a) Tìm điều kiện xác định và rút gọn biểu thức M

b) Tìm giá trị của x để M = 1/3.

c) Tìm giá trị lớn nhất của biểu thức P = M - 9√x

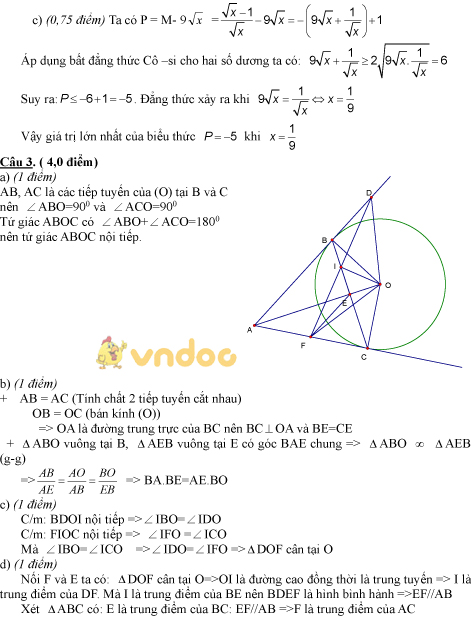
Câu 3. Cho đường tròn tâm O, từ điểm A ở ngoài đường tròn vẽ hai tiếp tuyến AB và AC (B,C là các tiếp điểm), OA cắt BC tại E.

a) Chứng minh tứ giác ABOC nội tiếp.

b) Chứng minh và BA.BE = AE.BO

c) Gọi I là trung điểm của BE, đường thẳng qua I và vuông góc với OI cắt tia AB, AC theo thứ tự tại D và F. Chứng minh tam giác DOF cân tại O.

d) Chứng minh F là trung điểm của AC.

Câu 4. Cho x, y là các số thực không âm thỏa mãn: x+y ≤1

Chứng minh rằng: x²y²(x²+y²)≤1/32

MÃ ĐỀ 02

Câu 1.

a) Tìm điều kiện của x để biểu thức sau có nghĩa: A=√1-x + √3+2x

b) Rút gọn biểu thức: B=√48 -2√27 - √(1-√3)²

c) Cho đường thẳng (d): y = 3x + m - 2. Tìm m để đường thẳng (d) cắt các trục tọa độ Ox, Oy lần lượt tại M và N sao cho MON có diện tích bằng 6

Câu 2. Cho biểu thức

a) Tìm điều kiện xác định và rút gọn biểu thức M

b) Tìm giá trị của x để M =1/2.

c) Tìm giá trị lớn nhất của biểu thức P = M - 8√x

Câu 3. Cho đường tròn tâm I, từ điểm M ở ngoài đường tròn vẽ hai tiếp tuyến MA và MB (A, B là các tiếp điểm), IM cắt AB tại N.

a) Chứng minh tứ giác MAIB nội tiếp.

c) Gọi K là trung điểm của AN, đường thẳng qua K và vuông góc với IK cắt tia MA, MB theo thứ tự tại G và H. Chứng minh tam giác GIH cân tại I.

d) Chứng minh H là trung điểm của MB.

Câu 4. Cho x, y là các số thực không âm thỏa mãn: x+y≤ 1

Chứng minh rằng: x²y²(x²+y²)≤1/32

ĐÁP ÁN THI THỬ VÀO LỚP 10 MÔN TOÁN (MÃ ĐỀ 01)