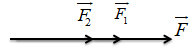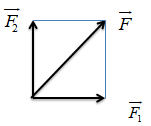Phương pháp giải một số dạng bài tập về tổng hợp và phân tích lực đồng quy theo quy tắc hình bình hành
Tổng hợp cách giải một số dạng bài tập về tổng hợp và phân tích lực đồng quy theo quy tắc hình bình hành
1. Tổng hợp lực là thay thế hai hay nhiều lực tác dụng đồng thời vào một vật bởi một lực sao cho tác dụng vẫn không thay đổi. Lực thay thế gọi là hợp lực.
Dạng 1: Tổng hợp hai lực
- Sử dụng quy tắc hình bình hành
- Sử dụng quy tắc hai lực cùng phương, cùng chiều
- Sử dụng quy tắc hai lực cùng phương, ngược chiều
Dạng 2: Tổng hợp ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)
Bước 1: Lựa hai cặp lực theo thứ tự ưu tiên cùng chiều hoặc ngược chiều hoặc vuông góc, tổng hợp chúng thành một lực tổng hợp \(\overrightarrow {{F_{12}}} \)
Bước 2: Tiếp tục tổng hợp lực \(\overrightarrow {{F_{12}}} \) với lực \(\overrightarrow {{F_3}} \) còn lại cho ra được lực tổng hợp cuối cùng \(\overrightarrow F \)
Áp dụng quy tắc hình bình hành
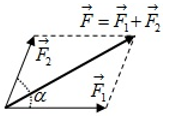
\(\left\{ \begin{array}{l}F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha } \\\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\end{array} \right.\)
*Ba trường hợp đặc biệt
+ Hai lực cùng phương, cùng chiều:
\(\overrightarrow {{F_1}} \uparrow \uparrow \overrightarrow {{F_2}} :\alpha = {0^0} \Rightarrow F = {F_1} + {F_2}\)
+ Hai lực cùng phương, ngược chiều:
\(\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_2}} :\alpha = {180^0} \Rightarrow F = \left| {{F_1} - {F_2}} \right|\)
+ Hai lực vuông góc:
\(\overrightarrow {{F_1}} \bot \overrightarrow {{F_2}} :\alpha = {90^0} \Rightarrow F = \sqrt {{F_1}^2 + {F_2}^2} \)
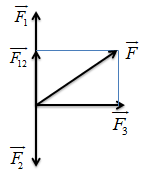
Bài tập ví dụ: Một chất điểm chịu các lực tác dụng có hướng như hình vẽ và có độ lớn lần lượt là \({F_1} = 60N,{F_2} = 30N,{F_3} = 40N\). Xác định hướng và độ lớn lực tổng hợp tác dụng lên chất điểm
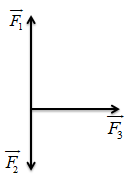
Hướng dẫn giải
Ta tổng hợp các lực như hình vẽ:
+ Tổng hợp hai lực cùng phương, ngược chiều \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) ta được lực \(\overrightarrow {{F_{12}}} \)
Suy ra ta có:
\(\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_2}} :\alpha = {180^0} \\\Rightarrow F = \left| {{F_1} - {F_2}} \right|\)= 60 – 30 = 30N
+ Tổng hợp hai lực \(\overrightarrow {{F_{12}}} ,\overrightarrow {{F_3}} \)theo quy tắc hình bình hành ta được lực tổng hợp \(\overrightarrow F \)
Ta có: \(\overrightarrow {{F_{12}}} \bot \overrightarrow {{F_3}} :\alpha = {90^0}\\ \Rightarrow F = \sqrt {{F_{12}}^2 + {F_3}^2} = \sqrt {{{30}^2} + {{40}^2}} = 50N\)
2. Phân tích lực (ngược với tổng hợp lực): là thay thế một lực bởi hai hay nhiều lực tác dụng đồng thời sao cho tác dụng vẫn không thay đổi.
Lưu ý: Phân tích lực là phép toán ngược lại với tổng hợp lực, do đó nó cũng tuẫn theo quy tắc hình bình hành. Tuy nhiên, chỉ khi biết một lực có tác dụng cụ thể theo hai phương nào thì mới phân tích lực đó theo hai phương ấy.
Bài tập ví dụ: Một vật nằm trên mặt nghiêng góc 300 so với phương ngang chịu tác dụng của trọng lực có độ lớn là 50 N. Xác định độ lớn các thành phần của trọng lực theo phương vuông góc và song song với mặt nghiêng.
Hướng dẫn giải
Ta phân tích trọng lực \(\overrightarrow P \) thành hai thành phần \(\overrightarrow {{P_1}} ,\overrightarrow {{P_2}} \) theo phương song song và vuông góc với mặt phẳng nghiêng như hình vẽ:
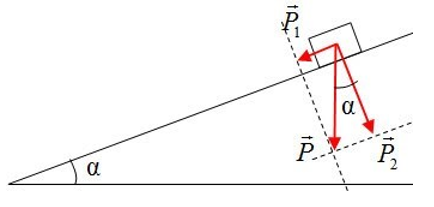
Từ hình vẽ ta có: \(\left\{ \begin{array}{l}{P_1} = P\sin \alpha = 50.\sin {30^0} = 25N\\{P_2} = P\cos \alpha = 50.\cos {30^0} = 25\sqrt 3 N\end{array} \right.\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Phương pháp giải một số dạng bài tập về tổng hợp và phân tích lực đồng quy theo quy tắc hình bình hành timdapan.com"