Phương pháp giải một số dạng bài tập về lực ma sát

Dạng 1: Tính lực ma sát, hệ số ma sát

- Bước 1: Phân tích lực

- Bước 2: Áp dụng định luật II Niuton để viết phương trình độ lớn của các lực

* Lực ma sát gồm ba loại thường gặp:

- Lực ma sát trượt: \({F_{m{\rm{s}}t}} = {\mu _t}.N\)

- Lực ma sát nghỉ: \({F_{m{\rm{s}}n}} = {F_t}\) ; \({F_t}\) là ngoại lực hoặc thành phần ngoại lực song song với bề mặt tiếp xúc.

\({F_{m{\rm{s}}n}}\max  = {\mu _n}.N\left( {{\mu _n} > {\mu _t}} \right)\)

- Lực ma sát lăn: \({F_{m{\rm{s}}l}} = {\mu _l}.N\)

Trong đó: \({\mu _t};{\mu _n};{\mu _l}\) lần lượt là hệ số ma sát trượt, hệ số ma sát nghỉ, hệ số ma sát lăn.

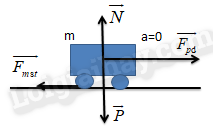
Ví dụ 1: Một ô tô khối lượng 1,5 tấn chuyển động thẳng đều trên đường. Hệ số ma sát giữa bánh xe và mặt đường là 0,08. Tính lực phát động đặt vào xe.

Hướng dẫn giải

Các lực tác dụng lên xe gồm: \(\overrightarrow P ;\overrightarrow N ;{\overrightarrow F _{m{\rm{s}}t}};{\overrightarrow F _{p{\rm{d}}}}\)

Chọn chiều dương cùng chiều chuyển động, phương trình định luật II Niuton viết cho vật là:

\({\overrightarrow F _{m{\rm{s}}t}} + {\overrightarrow F _{p{\rm{d}}}} + \overrightarrow N  + \overrightarrow P  = m\overrightarrow a \) (*)

Do ô tô chuyển động thẳng đều nên gia tốc a = 0. Chiếu phương trình (*) lên chiều dương ta được:

\(\left\{ \begin{array}{l} - {F_{m{\rm{s}}t}} + {F_{p{\rm{d}}}} = 0 \Leftrightarrow {F_{p{\rm{d}}}} = {F_{m{\rm{s}}t}} = \mu N\\N = P = mg\end{array} \right.\)

\( \Rightarrow {F_{p{\rm{d}}}} = \mu P = \mu mg = 0,08.1500.9,8 = 1176N\)

Dạng 2: Tính quãng đường, thời gian đi được khi có lực ma sát

- Bước 1: Chọn hệ quy chiếu: gốc tọa độ, mốc thời gian, chiều dương

- Bước 2: Phân tích lực

- Bước 3: Viết phương trình định luật II Niuton

- Bước 4: Chiếu phương trình lên chiều dương và tìm gia tốc của vật. Từ đó, suy ra quãng đường, thời gian vật đi được.

Ví dụ 2: Một xe điện đang chạy với vận tốc 36 km/h thì bị hãm lại đột ngột. Bánh xe không lăn nữa mà chỉ trượt lên đường ray. Kể từ lúc hãm, xe điện còn đi được bao xa thì dừng lại? Biết hệ số ma sát trượt giữa bánh xe và đường ray là 0,2. Lấy g = 9,8m/s².

Hướng dẫn giải

Đổi 36 km/h = 10 m/s

Kể từ lúc hãm xe, lực ma sát đóng vai tò cản trở chuyển động khiến xe dừng lại.

Chọn chiều dương cùng chiều chuyển động.

Áp dụng định luật II Niuton ta có:

\({\overrightarrow F _{m{\rm{s}}}} + \overrightarrow P  + \overrightarrow N  = m\overrightarrow a \) (*)

Chiếu phương trình (*) lên chiều dương ta được:

\( - {F_{m{\rm{s}}}} = ma \Leftrightarrow  - \mu mg = ma\\ \Leftrightarrow a =  - \mu g =  - 0,2.9,8 =  - 1,96m/{s^2}\)

Quãng đường vật đi được kể từ khi hãm phanh đến khi dừng hẳn là:

\(s = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{0^2} - {{10}^2}}}{{2.\left( { - 1,96} \right)}} = 25,51m\)

Dạng 3: Tính lực kéo để xe chuyển động khi có ma sát

- Khi xe chuyển động thẳng đều (a= 0) => \({F_{m{\rm{s}}}} = F\) (F là ngoại lực hoặc thành phần ngoại lực song song với bề mặt tiếp xúc)

- Khi xe chuyển động thẳng biến đổi đều:

+ Phân tích tất cả các lực tác dụng vào vật

+ Viết phương tình định luật II Niuton để xác định lực cần tìm.

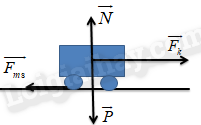
Ví dụ 3: Một ô tô khối lượng m = 1 tấn chuyển động nhanh dần đều trên mặt đường nằm ngang với gia tốc a = 2m/s². Hệ số ma sát giữa bánh xe và mặt đường là 0,1. Tính lực kéo của ô tô.

Hướng dẫn giải

Chọn chiều dương cùng chiều chuyển động của xe.

Các lực tác dụng lên xe gồm: \(\overrightarrow P ;\overrightarrow N ;{\overrightarrow F _{m{\rm{s}}}};\overrightarrow {{F_k}} \)

Áp dụng phương trình định luật II Niuton ta có:

\({\overrightarrow F _{m{\rm{s}}}} + {\overrightarrow F _k} + \overrightarrow N  + \overrightarrow P  = m\overrightarrow a \) (*)

Chiếu phương trình (*) lên chiều dương, ta có:

\( - {F_{m{\rm{s}}}} + {F_k} = ma\\ \Rightarrow {F_k} = {F_{m{\rm{s}}}} + ma = \mu mg + ma\)

Thay số:

\({F_k} = 0,1.1000.10 + 1000.2 = 3000N\)

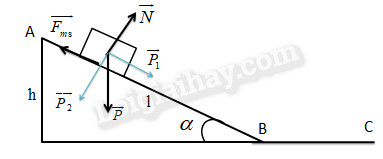
Dạng 4: Tính vận tốc của vật ở chân mặt phẳng nghiêng có ma sát

- Vật đang đứng yên trên mặt phẳng nghiêng: a = 0

\( \Rightarrow {F_{m{\rm{s}}n}} = {P_1} = mg\sin \alpha \)

- Điều kiện để vật trượt xuống: a > 0

\({P_1} > {F_{m{\rm{s}}}} \Rightarrow mg\sin \alpha  > \mu mg\cos \alpha  \Rightarrow \mu  < \tan \alpha \)

- Chọn chiều dương cùng chiều chuyển động. Áp dụng định luật II Niuton và chiếu lên chiều dương ta được:

\({P_1} - {F_{m{\rm{s}}}} = ma\)

+ Khi đó, vật trượt xuống với gia tốc:

\(\begin{array}{l}a = \frac{{{P_1} - {F_{m{\rm{s}}}}}}{m} = \frac{{mg\sin \alpha  - \mu mg.\cos \alpha }}{m}\\ = g\sin \alpha  - \mu g\cos \alpha \end{array}\)

+ Vận tốc của vật ở chân mặt phẳng nghiêng:

\(v = \sqrt {2{\rm{a}}s}  = \sqrt {\frac{{2gh\left( {\sin \alpha  - \mu \cos \alpha } \right)}}{{\sin \alpha }}} \)

Ví dụ 4: Vật đặt trên đỉnh dốc dài 165m, hệ số ma sát 0,2, góc nghiêng dốc là \(\alpha \).

a) Với giá trị nào của \(\alpha \) thì vật nằm yên không trượt?

b) Cho \(\alpha  = {30^0}\). Tìm vận tốc vật ở chân dốc.

Cho \(\tan {11^0} = 0,2;\cos {30^0} = 0,85\).

Hướng dẫn giải

a) Để vật nằm yên không trượt thì:

\(\tan \alpha  \le \mu  \Leftrightarrow \tan \alpha  \le 0,2 \Leftrightarrow \alpha  \le {11^0}\)

b) Vận tốc khi vật ở chân dốc là:

\(v = \sqrt {2{\rm{a}}s}  = \sqrt {\frac{{2gh\left( {\sin \alpha  - \mu \cos \alpha } \right)}}{{\sin \alpha }}}  \\= \sqrt {\frac{{2.10.165\left( {\sin {{30}^0} - 0,2.\cos {{30}^0}} \right)}}{{\sin {{30}^0}}}}  = 33m/s\)