Phương pháp giải một số dạng bài tập về lực hướng tâm
Tổng hợp cách giải một số dạng bài tập về lực hướng tâm hay, chi tiết
Dạng 1: Tính lực hướng tâm
Vận dụng các công thức trong chuyển động tròn đều:
- Chu kì: \(T = \frac{{2\pi }}{\omega }\)
- Tần số: \(f = \frac{1}{T} = \frac{\omega }{{2\pi }}\)
- Tốc độ góc: \(\omega = \frac{v}{r} = \frac{{2\pi }}{T} = \frac{f}{{2\pi }}\)
- Lực hướng tâm: \({F_{ht}} = m.{a_{ht}}\)
- Gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r} = r.{\omega ^2}\)
- Công thức liên hệ giữa tốc độ dài và tốc độ góc: \(v = r\omega \)
Ví dụ 1: Xe đạp của một vận động viên chuyển động thẳng đều với v = 36km/h. Biết bán kính của lốp bánh xe là 40cm. Tính tốc độ góc và gia tốc hướng tâm tại một điểm trên lốp bánh xe.
Hướng dẫn giải
Vận tốc xe đạp cũng là tốc độ dài của một điểm trên lốp xe:
v = 36km/h = 10m/s
Tốc độ góc: \(\omega = \frac{v}{r} = \frac{{10}}{{0,4}} = 25{\rm{r}}a{\rm{d}}/s\)
Gia tốc hướng tâm tại một điểm trên lốp bánh xe là:
\({a_{ht}} = \frac{{{v^2}}}{r} = 250m/{s^2}\)
Dạng 2: Tính áp lực của vật tại điểm cao nhất của vòng cầu
- Bước 1: Xác định vecto lực hướng tâm.
+ Vẽ hình, tìm tất cả các lực tác dụng vào vật chuyển động tròn.
+ Tổng hợp các lực đó theo phương bán kính hướng vào tâm đó là lực hướng tâm.
- Bước 2: Viết biểu thức tính độ lớn lực hướng tâm theo m và aht
- Bước 3: Đồng nhất biểu thức lực và biểu thức độ lớn tìm ẩn số.
* Cụ thể với bài toán tính áp lực vật tại điểm cao nhất của vòng cầu thì:
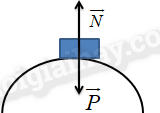
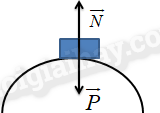
Cầu vồng lên:
\(P - N = m{a_{ht}} \Leftrightarrow N = P - {F_{ht}}\)
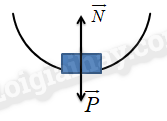
Cầu vồng xuống (cầu lõm):
\(N - P = m{a_{ht}} \Leftrightarrow N = P + {F_{ht}}\)
* Chuyển động của xe đi vào khúc quanh (mặt đường phải làm nghiêng): lực hướng tâm là hợp lực của phản lực \(\overrightarrow N \) và trọng lực \(\overrightarrow P \)
Ví dụ 2: Một ô tô khối lượng 2,5 tấn chuyển động qua một cầu vượt với vận tốc không đổi là 54 km/h. Cầu vượt có dạng một cung tròn, bán kính 100 m. Tính áp lực của ô tô lên cầu tại điểm cao nhất của cầu. Lấy g = 9,8 m/s2.
Hướng dẫn giải
Ta có:
R = 100 m
m = 2500 kg
v = 15 m/s
Khi ô tô đến điểm cao nhất thì một phần của trọng lực đóng vai trò là lực hướng tâm.
Chọn chiều dương hướng vào tâm.
Áp dụng định luật II Niuton ta có:
\(\overrightarrow N + \overrightarrow P = m{\overrightarrow a _{ht}}\) (*)
Chiếu phương trình (*) lên chiều dương ta được:
\(P - N = {F_{ht}} \Rightarrow N = P - {F_{ht}}\)
Tại điểm cao nhất lực ép của xe lên cầu là:
\(N = mg - \frac{{m{v^2}}}{R} = 2500.9,8 - \frac{{{{2500.15}^2}}}{{100}} = 18875N\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Phương pháp giải một số dạng bài tập về lực hướng tâm timdapan.com"