Phương pháp giải một số dạng bài tập về con lắc lò xo

Dạng 1: Tính chu kì, tần số của con lắc lò xo

Sử dụng các công thức:

+ Tần số góc: \(\omega  = \sqrt {\frac{k}{m}}  = \sqrt {\frac{g}{{\Delta {l_0}}}}  = \frac{{2\pi }}{T} = 2\pi f\)

+ Chu kì: \(T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \)

+ Tần số: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}  = \frac{1}{{2\pi }}\sqrt {\frac{g}{{\Delta {l_0}}}} \)

Với \(\Delta {l_0} = \frac{{mg}}{k}\) là độ biến dạng của lò xo khi vật ở vị trí cân bằng.

*Bài toán ghép vật

- Lò xo K gắn vật nặng m₁ thì dao động với chu kì T₁. Còn khi gắn vật nặng m₂ thì dao động với chu kì T₂. Chu kì dao động của vật khi gắn vật có khối lượng m = m₁ + m₂ là:

\({T^2} = T_1^2 + T_2^2\)

Tổng quát:

+ Chu kì dao động của vật khi gắn vật có khối lượng \(m = {m_1} + {m_2} + ... + {m_n}\) là:

\({T^2} = T_1^2 + T_2^2 + ... + T_n^2\)

+ Chu kì dao động của vật khi gắn vật có khối lượng m = a.m₁ + b.m₂ là:

\({T^2} = aT_1^2 + bT_2^2\)

- Lò xo K gắn vật nặng m₁ thì dao động với chu kì f₁. Còn khi gắn vật nặng m₂ thì dao động với chu kì f₂. Tần số dao động của vật khi gắn vật có khối lượng m = m₁ + m₂ là:

\(f = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }}\)

Tổng quát:

+ Tần số dao động của vật khi gắn vật có khối lượng \(m = {m_1} + {m_2} + ... + {m_n}\) là:

\(\frac{1}{{{f^2}}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} + ... + \frac{1}{{f_n^2}}\)

+ Tần số dao động của vật khi gắn vật có khối lượng m = a.m₁ + b.m₂ là:

\(\frac{1}{{{f^2}}} = \frac{{{a}}}{{f_1^2}} + \frac{{{b}}}{{f_2^2}}\)

Bài tập ví dụ:

Bài 1: Một con lắc lò xo nằm ngang có độ cứng k = 100 N/m được gắn vào vật nặng có khối lượng m = 0,1 kg. Kích thích cho vật dao động điều hòa, xác định chu kì của con lắc lò xo.

Hướng dẫn giải

 Ta có:

\(\left\{ \begin{array}{l}m = 0,1kg\\k = 100N/m\end{array} \right. \Rightarrow T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{0,1}}{{100}}}  = 0,2 {\rm{s}}\)

Bài 2: Một lò xo có độ cứng là k. Khi gắn vậ m₁ vào lò xo và cho dao động thì chu kì là 0,3 s. Khi gắn vật có khối lượng m₂ vào lò xo trên và kích thích cho dao động thì nó dao động với chu kì là 0,4s. Hỏi nếu khi gắn vật có khối lượng m = 2m₁ + 3m₂ thì nó dao động với chu kì là bao nhiêu?

Hướng dẫn giải

Khi đó chu kì dao động của vật là:

\({T^2} = 2T_1^2 + 3T_2^2 \\\Leftrightarrow T = \sqrt {2T_1^2 + 3T_2^2}  \\= \sqrt {2.0,{3^2} + 3.0,{4^2}}  = 0,812s\)

Dạng 2: Tính chiều dài con lắc lò xo, lực đàn hồi, lực phục hồi

*Chiều dài con lắc lò xo

Gọi l₀ là chiều dài tự nhiên của con lắc lò xo, l_cb là chiều dài của con lắc lò xo ở vị trí cân bằng, \(\Delta {l_0}\) là độ biến dạng của lò xo khi ở VTCB. Ta có: \({l_{cb}} = {l_0} + \Delta {l_0}\)

Chọn gốc tọa độ tại VTCB, chiều dương hướng xuống dưới, ta có:

+ Chiều dài cực đại (khi vật ở vị trí thấp nhất): \({l_{\max }} = {l_0} + \Delta {l_0} + A\)

+ Chiều dài cực tiểu (khi vật ở vị trí cao nhất): \({l_{\min }} = {l_0} + \Delta {l_0} - A\)

\( \Rightarrow {l_{cb}} = \frac{{{l_{\max }} + {l_{\min }}}}{2}\)

*Lực đàn hồi: \({F_{dh}} = k\left( {\Delta {l_0} + x} \right)\)

- Lực đàn hồi cực đại: \({F_{\max }} = k\left( {\Delta l + A} \right)\)

- Lực đàn hồi cực tiểu:

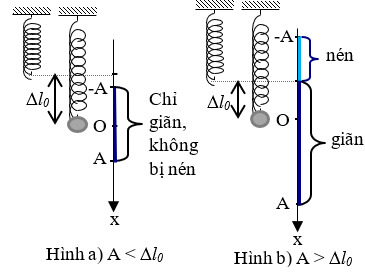
+ Nếu \(A < \Delta l \Rightarrow {F_{dh\min }} = k\left( {\Delta l - A} \right)\)

+ Nếu \(A \ge \Delta l \Rightarrow {F_{dh\min }} = 0\)( lúc vật đi qua vị trí lò xo không biến dạng)

*Lực phục hồi (lực kéo về)

\({F_{ph}} = ma = m\left( { - {\omega ^2}x} \right) =  - k{\rm{x}}\)

Trong trường hợp lò xo treo thẳng đứng lực đàn hồi và lực phục hồi khác nhau.

Trong trường hợp \(A > \Delta {l_0}\):

+ \({F_{nen}} = k\left( {\left| x \right| - \Delta {l_0}} \right),\left| x \right| \ge \Delta {l_0}\)

+ \({F_{nen\max }} = k\left| {A - \Delta {l_0}} \right|\)

Bài tập ví dụ: Một con lắc lò xo có chiều dài tự nhiên là 30 cm, độ cứng của lò xo là k = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5cm. Xác định lực đàn hồi cực đại, cực tiểu của lò xo trong quá trình dao động của vật.

Hướng dẫn giải

Độ biến dạng của lò xo khi vật ở VTCB là:

\(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,1.10}}{{10}} = 0,1m\)

Lực đàn hồi cực đại:

\({F_{\max }} = k\left( {\Delta {l_0} + A} \right) = 10.\left( {0,1 + 0,05} \right) = 1,5N\)

Lực đàn hồi cực tiểu:

\({F_{\min }} = k\left( {\Delta l - A} \right) = 10.\left( {0,1 - 0,05} \right) = 0,5N\)