Lý thuyết thể tích của hình hộp chữ nhật

A. KIẾN THỨC CƠ BẢN

1. Đường thẳng vuông góc với mặt phẳng

Hai mặt phẳng vuông góc

a) Đường thẳng vuông góc với mặt phẳng

Nếu một đường thẳng vuông góc với một mặt phẳng tại điểm \(A\) thì nó vuông góc với mọi đường thẳng của mặt phẳng đi qua \(A.\)

b) Hai mặt phẳng vuông góc

Khi một trong hai mặt phẳng \((ABCD)\) và \((A'B'C'D')\) chứa một đường thẳng vuông góc với mặt phẳng còn lại thì người ta nói hai mặt phẳng đó vuông góc với nhau.

Kí hiệu : \(mp (ABCD)⊥ mp ( (A'B'C'D')\)

Hình minh họa

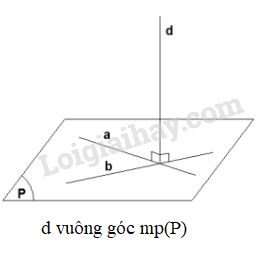
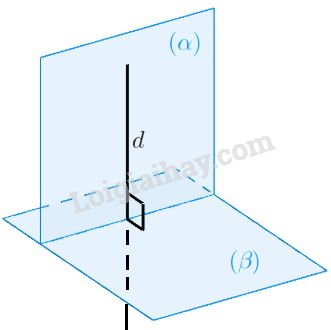
\(mp\left( \alpha  \right) \bot mp\left( \beta  \right)\)

2. Thể tích hình hộp chữ nhật 

\(V = a.b.c\)

\(a, b, c\) là ba kích thước của hình hộp

Thể tích hình lập phương cạnh \(a\) là:

\(V =a^3\)