Lý thuyết Nhân, chia phân thức SGK Toán 8 - Chân trời sáng tạo
Nhân hai phân thức
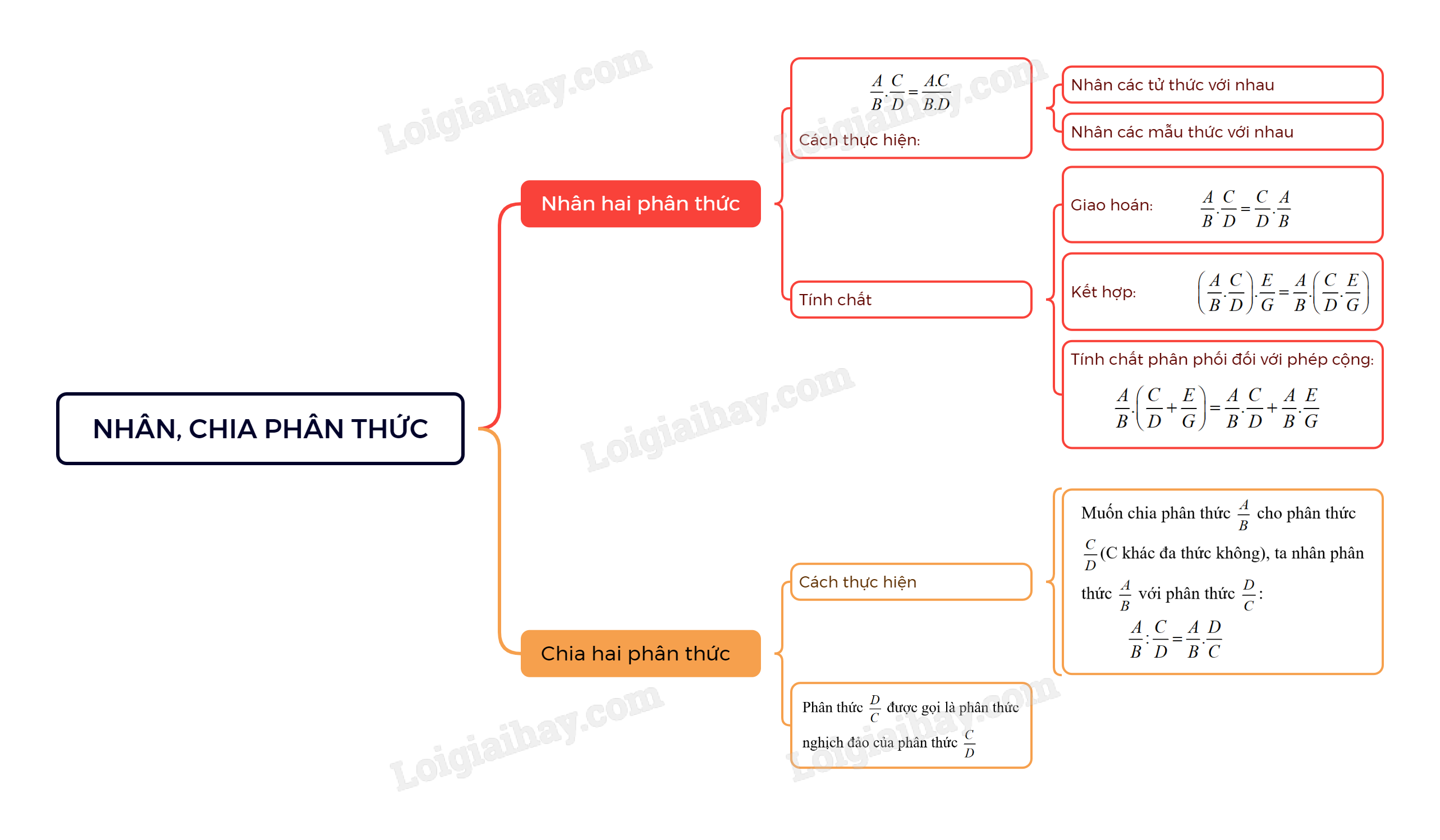
1. Nhân hai phân thức
Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau.
\(\frac{A}{B}.\frac{C}{D} = \frac{{A.C}}{{B.D}}\)
2. Tính chất
- Giao hoán: \(\frac{A}{B}.\frac{C}{D} = \frac{C}{D}.\frac{A}{B}\)
- Kết hợp: \(\left( {\frac{A}{B}.\frac{C}{D}} \right).\frac{E}{G} = \frac{A}{B}.\left( {\frac{C}{D}.\frac{E}{G}} \right)\)
- Tính chất phân phối đối với phép cộng: \(\frac{A}{B}.\left( {\frac{C}{D} + \frac{E}{G}} \right) = \frac{A}{B}.\frac{C}{D} + \frac{A}{B}.\frac{E}{G}\)
Ví dụ:
\(\frac{{2xz}}{{3y}}.\frac{{ - 6{y^3}}}{{8{x^2}z}} = \frac{{2xz.( - 6{y^3})}}{{3y.8{x^2}z}} = \frac{{ - {y^2}}}{{2x}}\);
\(\frac{{{x^2} - 1}}{{{x^2} + 4x}}.\frac{{2x}}{{x - 1}} = \frac{{(x - 1)(x + 1).2x}}{{x(x + 4)(x - 1)}} = \frac{{2(x + 1)}}{{x + 4}}\)
3. Chia hai phân thức
Muốn chia phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\)(C khác đa thức không), ta nhân phân thức \(\frac{A}{B}\) với phân thức \(\frac{D}{C}\): \(\frac{A}{B}:\frac{C}{D} = \frac{A}{B}.\frac{D}{C}\)
Nhận xét: Phân thức \(\frac{D}{C}\) được gọi là phân thức nghịch đảo của phân thức \(\frac{C}{D}\)
Ví dụ:
\(\begin{array}{l}\frac{{{x^2} - 9}}{{x - 2}}:\frac{{x - 3}}{x} = \frac{{(x - 3)(x + 3)}}{{x - 2}}.\frac{x}{{x - 3}} = \frac{{(x - 3)(x + 3).x}}{{(x - 2)(x - 3)}} = \frac{{x(x + 3)}}{{x - 2}}\\\frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}:\frac{{{x^3}}}{{yz}} = \frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}.\frac{{yz}}{{{x^3}}} = \frac{{x.xz.yz}}{{{z^2}.{y^3}.{x^3}}} = \frac{{{x^2}y{z^2}}}{{{x^3}{y^3}{z^2}}} = \frac{1}{{x{y^2}}}\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Nhân, chia phân thức SGK Toán 8 - Chân trời sáng tạo timdapan.com"







