Luyện tập 2 trang 138 Tài liệu dạy – học Toán 8 tập 1
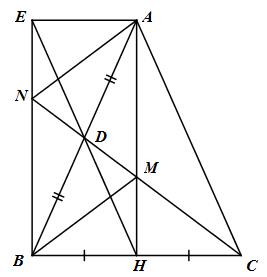
Giải bài tập Cho tam giác ABC cân tại A. Họ H, D lần lượt là trung điểm của các cạnh BC và AB.
Đề bài
Cho tam giác ABC cân tại A. Họ H, D lần lượt là trung điểm của các cạnh BC và AB.
a) Chứng minh rằng tứ giác ADHC là hình thang.
b) Gọi E là điểm đối xứng với H qua D. CHứng minh rằng tứ giác AHBE là hình chữ nhật.
c) Tia CD cắt AH ở M và cắt BE ở N. Chứng minh tứ giác AMBN là hình bình hành.
Lời giải chi tiết
a) Ta có D, H lần lượt là trung điểm của AB và BC.
\( \Rightarrow DH\) là đường trung bình của tam giác ABC.
\( \Rightarrow DH//AC \Rightarrow \) Tứ giác ADHC là hình thang.
b) \(\Delta ABC\) cân tại A có AH là đường trung tuyến (H là trung điểm của BC)
\( \Rightarrow AH\) là đường cao của tam giác ABC.
\( \Rightarrow AH \bot BC\) tại H.
Tứ giác AHBE có AB và EH cắt nhau tại D (gt)
D là trung điểm của AB (gt)
D là trung điểm của EH (E là điểm đối xứng với H qua D),
\(\widehat {NED} = \widehat {DHM}\) (hai góc so le trong và EB // AH)
Và \(\widehat {EDN} = \widehat {HDM}\) (hai góc đối đỉnh), do đó \(\Delta END = \Delta HDM\,\,\left( {g.c.g} \right)\)
\( \Rightarrow ND = MD \Rightarrow D\) là trung điểm của NB \(\left( {D \in NM} \right)\)
Mặt khác D là trung điểm của AB (gt) và NM, AB cắt nhau tại D (gt)
Do đó tứ giác AMBN là hình bình hành (dấu hiệu nhận biết hình bình hành)
Search google: "từ khóa + timdapan.com" Ví dụ: "Luyện tập 2 trang 138 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"