Hoạt động 4 trang 125 Tài liệu dạy – học Toán 9 tập 1

Đề bài

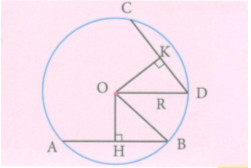
Cho đường tròn (O) và hai dây AB, CD khác đường kính. Từ O hạ OH và OK theo thứ tự vuông góc với AB và CD.

Hãy  điền vào chỗ chấm (…) để chứng minh :

Nếu AB = CD thì OH = OK.

Xét hai tam giác vuông OHB và OKD, ta có :

OB = OD (…………..)

HB = KD (…………..)

Suy ra \(\Delta OHB = \Delta OKD\)

Do đó OH = OK.

Lời giải chi tiết

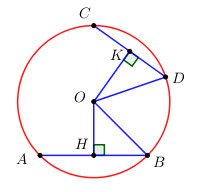
Xét hai tam giác vuông OHB và OKD có:

\(OB = OD\) (cùng bằng bán kính của \(\left( O \right)\))

\(HB = KD\) (do \(HB = \dfrac{1}{2}AB,\,\,KD = \dfrac{1}{2}CD,\)\(\,\,AB = CD\,\,\left( {gt} \right)\))

Suy ra \(\Delta OHB = \Delta OKD\) (cạnh góc vuông – cạnh huyền)

Do đó \(OH = OK\) (2 cạnh tương ứng)