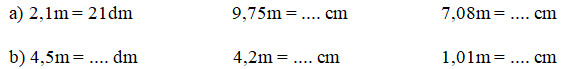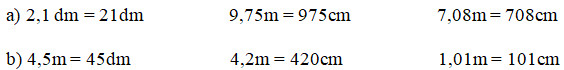Bài 35 : Luyện tập
Giải bài tập 1, 2, 3, 4 trang 47, 48 VBT toán 5 bài 35 : Luyện tập với lời giải chi tiết và cách giải nhanh, ngắn nhất
Bài 1
Chuyển các phân số thập phân thành số thập phân (theo mẫu) :
a) \( \displaystyle {{162} \over {10}} = 16{2 \over {10}} = 16,2;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad\)\( \displaystyle {{975} \over {10}} = .....= .....\)
b) \( \displaystyle {{7409} \over {100}} = ..... =.....;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad \)\( \displaystyle{{806} \over {100}} = ..... = .....\)
Phương pháp giải:
Quan sát ví dụ mẫu và làm tương tự với các câu còn lại.
Lưu ý: Để viết phân số dưới dạng hỗn số ta có thể lấy tử số chia cho mẫu số. Thương tìm được là số nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia.
Lời giải chi tiết:
a) \( \displaystyle {{162} \over {10}} = 16{2 \over {10}} = 16,2\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\) \( \displaystyle {{975} \over {10}} = 97{5 \over {10}} = 97,5.\)
b) \( \displaystyle {{7409} \over {100}} = 74{9 \over {100}} = 74,09\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\) \( \displaystyle {{806} \over {100}} = 8{6 \over {100}} = 8,06.\)
Bài 2
Chuyển các phân số thập phân thành số thập phân :
a) \( \displaystyle {{64} \over {10}} = ....;\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{372} \over {10}} = ....;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)\( \displaystyle{{1954} \over {100}} = ....\)
b) \( \displaystyle {{1942} \over {100}} = ....;\,\,\,\,\,\,\,\,\,\,\,\,{{6135} \over {1000}} = ....;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)\( \displaystyle{{2001} \over {1000}} = ....\)
Phương pháp giải:
Có thể chuyển phân số thập phân đã cho dưới dạng hỗn số rồi viết thành số thập phân.
Lời giải chi tiết:
a) \( \displaystyle {{64} \over {10}} =6\dfrac{4}{10}= 6,4;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\quad \)\( \displaystyle{{372} \over {10}} =37\dfrac{2}{10}= 37,2;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\) \( \displaystyle{{1954} \over {100}} =19\dfrac{54}{100}= 19,54\)
b) \( \displaystyle {{1942} \over {100}} =19\dfrac{42}{100}= 19,42;\,\,\,\,\,\,\,\,\,\,\,\,\,\)\( \displaystyle{{6135} \over {1000}} =61\dfrac{35}{100}= 6,135;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\) \( \displaystyle{{2001} \over {1000}} =2\dfrac{1}{1000}= 2,001\)
Bài 3
Viết số thích hợp vào chỗ trống (theo mẫu)
Phương pháp giải:
Ta có thể làm như sau: \(\displaystyle 2,1m = 2{1 \over {10}}m = 2m\,\,1dm = 21dm\).
Các câu khác làm tương tự như câu trên.
Lời giải chi tiết:
+) \( \displaystyle 2,1m = 2{1 \over {10}}m = 2m\,\,1dm = 21dm\)
+) \( \displaystyle 9,75m = 9\,{{75} \over {100}}\,m = 9m\;75cm \) \(=975cm\)
+) \( \displaystyle 7,08m = 7\,{{8} \over {100}}\,m = 7m\;8cm \) \(= 708cm\).
+) \( \displaystyle 4,5m = 4\,{5 \over {10}}\,m = 4m\;5dm =45dm\)
+) \( \displaystyle 4,2m = 4\,{{2} \over {10}}\,m =4\,\dfrac{20}{100}m \) \(= 4m\;20cm =420cm\)
+) \( \displaystyle 1,01m = 1\,{{1} \over {100}}\,m = 1m\;1cm \) \(= 101cm\).
Vậy ta có kết quả như sau :
Bài 4
Viết tiếp vào chỗ chấm cho thích hợp
\( \displaystyle {9 \over {10}} = 0,9\,\,\,;\,\,{{90} \over {100}} = 0,90\)
Ta thấy: \(0,9 = 0,90\) vì ...........................
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số : nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Ta có : \( \displaystyle {9 \over {10}} = 0,9\,\,\,;\,\,\quad \quad \quad \quad {{90} \over {100}} = 0,90\)
Ta thấy: \(0,9 = 0,90\) vì \( \displaystyle {9 \over {10}} = {9 \times 10 \over {10 \times 10 }}={{90} \over {100}}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 35 : Luyện tập timdapan.com"