Phần câu hỏi bài 8 trang 50 Vở bài tập toán 7 tập 2

Câu 22.

Khoanh tròn vào chữ cái trước đa thức mà em cho là kết quả đúng.

Phương pháp giải :

Dựa vào quy tắc dấu ngoặc và tính chất của các phép tính trên số, ta có thể cộng, trừ hai đa thức cũng như cộng, trừ các biểu thức số.

Cách giải :

\(\left( {{x^3} + 2{x^2} - 3x + 3} \right) - \)\(\left( {2{x^3} - 2{x^2} + 3x + 5} \right)\)

\( = {x^3} + 2{x^2} - 3x + 3 - 2{x^3} + 2{x^2} \)\(\,- 3x - 5\)

\( = \left( {{x^3} - 2{x^3}} \right) + \left( {2{x^2} + 2{x^2}} \right) \)\(+ \left( { - 3x - 3x} \right) + \left( {3 - 5} \right)\)

\( =  - {x^3} + 4{x^2} - 6x - 2\)

Chọn B.

Câu 23.

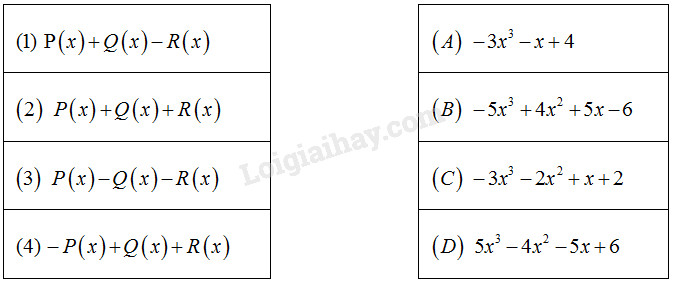
Cho \(P(x) = {x^3} - 2{x^2} - 3x + 5;\)\(\,\,Q\left( x \right) =  - 4{x^3} + {x^2} + 3x - 2\); \(R\left( x \right) = {x^2} - x + 1.\) Nối biểu thức ở cột bên trái với đa thức ở cột bên phải để được đẳng thức đúng :

Phương pháp giải :

Thực hiện phép tính với các đa thức rồi nối biểu thức ở cột bên trái với ô trống thích hợp ở cột bên phải.

Cách giải:

\(P\left( x \right) + Q\left( x \right) - R\left( x \right)\)

\(= \left( {{x^3} - 2{x^2} - 3x + 5} \right) \)\(\,+ \left( { - 4{x^3} + {x^2} + 3x - 2} \right)\)\(\, - \left( {{x^2} - x + 1} \right)\)

\(= {x^3} - 2{x^2} - 3x + 5 - 4{x^3} + {x^2} + 3x\)\(\, - 2 - {x^2} + x - 1\)

\(= \left( {{x^3} - 4{x^3}} \right) \)\(\,+ \left( { - 2{x^2} + {x^2} - {x^2}} \right) \)\(\,+ \left( { - 3x + 3x + x} \right) + \left( {5 - 2 - 1} \right)\)

\(= - 3{x^3} - 2{x^2} + x + 2\)

\(P\left( x \right) + Q\left( x \right) + R\left( x \right)\)

\(= \left( {{x^3} - 2{x^2} - 3x + 5} \right) \)\(\,+ \left( { - 4{x^3} + {x^2} + 3x - 2} \right)\)\(\, + \left( {{x^2} - x + 1} \right)\)

\(= {x^3} - 2{x^2} - 3x + 5 - 4{x^3} + {x^2} + 3x \)\(\,- 2 + {x^2} - x + 1\)

\(= \left( {{x^3} - 4{x^3}} \right) \)\(\,+ \left( { - 2{x^2} + {x^2} + {x^2}} \right) \)\(\,+ \left( { - 3x + 3x - x} \right) + \left( {5 - 2 + 1} \right)\)

\(= - 3{x^3} - x + 4\)

\(P\left( x \right) - Q\left( x \right) - R\left( x \right) \)

\(= \left( {{x^3} - 2{x^2} - 3x + 5} \right) \)\(\,- \left( { - 4{x^3} + {x^2} + 3x - 2} \right)\)\(\,- \left( {{x^2} - x + 1} \right)\)

\(= {x^3} - 2{x^2} - 3x + 5 + 4{x^3} - {x^2} - 3x \)\(\,+ 2 - {x^2} + x - 1\)

\(= \left( {{x^3} + 4{x^3}} \right) + \left( { - 2{x^2} - {x^2} - {x^2}} \right)\)\(\, + \left( { - 3x - 3x + x} \right) + \left( {5 + 2 - 1} \right)\)

\(= 5{x^3} - 4{x^2} - 5x + 6\)

\(\begin{array}{l}
- P\left( x \right) + Q\left( x \right) + R\left( x \right)\\
= - \left[ {P\left( x \right) - Q\left( x \right) - R\left( x \right)} \right]\\
= - \left( {5{x^3} - 4{x^2} - 5x + 6} \right)\\
= - 5{x^3} + 4{x^2} + 5x - 6
\end{array}\)

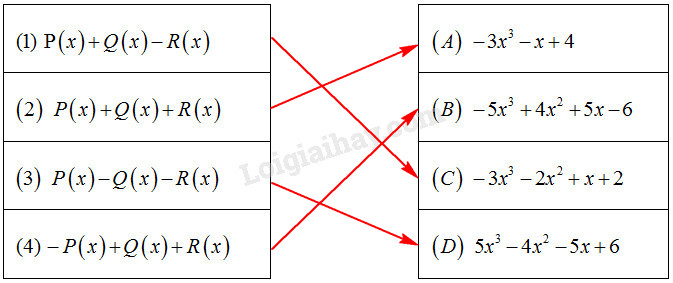
Ta nối như sau:

Câu 24.

Khoanh tròn vào chữ cái trước khẳng định đúng.

Cho \(P(x), Q(x), R(x)\) như ở câu 23 thì bậc của đa thức

(A) \(–P(x) – Q(x) + R(x)\) là \(2\);

(B) \(–P(x) – Q(x) – R(x)\) là \(3\);

(C) \(–P(x) + Q(x) + R(x)\) là \(2\).

Phương pháp giải :

- Thực hiện phép tính với các đa thức.

- Tìm bậc rồi chọn đáp án đúng nhất.

Cách giải :

Ta có : 

\(P\left( x \right) + Q\left( x \right) + R\left( x \right) \)\(\,=  - 3{x^3} - x + 4\) (câu 23)

\(–P(x) – Q(x) – R(x)\) \(= -[P(x) + Q(x) + R(x)]\) \(=3{x^3} +x - 4\)

Bậc của đa thức là \(3\).

Chọn B.