Phần câu hỏi bài 7 trang 113, 114 Vở bài tập toán 8 tập 1

Câu 17.

Tứ giác \(ABCD\) là hình bình hành nếu

(A) \(AB=CD\) 

(B) \(AD=BC\)

(C) \(AB//CD\) và \(AD=BC\)

(D) \(AB=CD\) và \(AD=BC\).

Khoanh tròn vào chữ cái trước câu trả lời đúng.

Phương pháp giải:

Dấu hiệu nhận biết: Tứ giác có các cạnh đối bằng nhau là hình bình hành.

Lời giải:

Chọn D.

Câu 18.

Hình thang \(ABCD(AB//CD)\) là hình bình hành nếu

(A) \(AB=CD\)

(B) \(AD=BC\)

(C) \(AD//BC\)

(D) \(\widehat A + \widehat B = {180^o}\)

Khoanh tròn vào chữ cái trước câu trả lời không đúng.

Phương pháp giải:

Dấu hiệu nhận biết hình bình hành: 

a) Tứ giác có các cạnh đối song song là hình bình hành.

b) Tứ giác có các cạnh đối bằng nhau là hình bình hành.

c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

d) Tứ giác có các góc đối bằng nhau là hình bình hành.

e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Lời giải:

Đáp án A. Tứ giác \(ABCD\) có \(AB//CD\) và \(AB=CD\) nên là hình bình hành.

Đáp án B. Hình thang \(ABCD\) có hai cạnh bên bằng nhau có thể không là hình bình hành mà là hình thang cân.

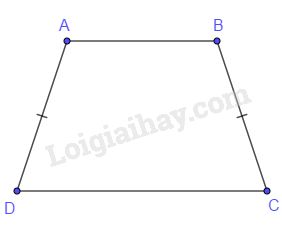
Đáp án C. Tứ giác \(ABCD\) có các cặp cạnh đối song song nên là hình bình hành.

Đáp án D. 

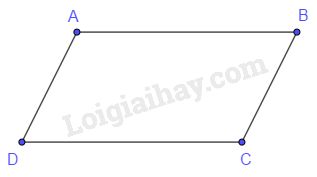
\(\widehat A + \widehat B = {180^o}\) mà hai góc ở vị trí trong cùng phía nên \(AD//BC\). Do đó tứ giác \(ABCD\) là hình bình hành.

Chọn B.

Câu 19.

Tứ giác \(ABCD\) là hình bình hành nếu

\(\eqalign{
& (A)\,\,\widehat A = {100^o},\,\,\widehat B = {80^o},\,\widehat C = {100^o} \cr
& (B)\,\,\widehat A = {95^o},\,\widehat B = {85^o},\,\widehat C = {85^o} \cr
& (C)\,\,\widehat A = {85^o},\widehat C = {85^o},\widehat D = {90^o} \cr
& (D)\,\,\widehat A = {70^o},\widehat B = {110^o},\widehat D = {90^o} \cr} \)

Khoanh tròn vào chữ cái trước câu trả lời đúng.

Phương pháp giải:

Áp dụng:

- Định lí tổng các góc của một tứ giác bằng \(360^o\)

- Dấu hiệu nhận biết hình bình hành: Tứ giác có các góc đối bằng nhau.

Lời giải:

Áp dụng đinh lí tổng các góc của một tứ giác bằng \(360^o\) ta được:

a) 

\(\eqalign{
& \widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right) \cr
& = {360^o} - \left( {{{100}^o} + {{80}^o} + {{100}^o}} \right) = {80^o} \cr} \)

b)

\(\eqalign{
& \widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right) \cr
& = {360^o} - \left( {{{95}^o} + {{85}^o} + {{85}^o}} \right) = {95^o} \cr} \)

c) 

\(\eqalign{
& \widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right) \cr
& = {360^o} - \left( {{{85}^o} + {{85}^o} + {{90}^o}} \right) = {100^o} \cr} \)

d) 

\(\eqalign{
& \widehat D = {360^o} - \left( {\widehat A + \widehat B + \widehat C} \right) \cr
& = {360^o} - \left( {{{70}^o} + {{110}^o} + {{90}^o}} \right) = {90^o} \cr} \)

Đáp án A. Tứ giác \(ABCD\) có các góc đối bằng nhau.

Chọn A.