Bài 32 trang 116 Vở bài tập toán 8 tập 1
Giải bài 32 trang 116 VBT toán 8 tập 1. Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao?
Đề bài
Tứ giác \(ABCD\) có \(E, F, G, H\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CD, DA.\) Tứ giác \(EFGH\) là hình gì ? Vì sao?
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Dấu hiệu nhận biết hình bình hành: Tứ giác cặp cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
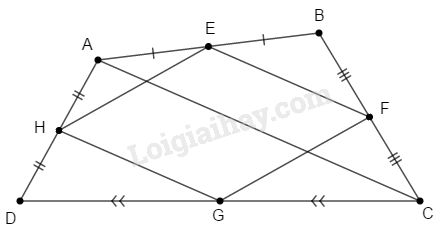

\(\Delta ABC\) có \(EA=EB\) và \( FB=FC\) nên \(EF\) là đường trung bình của \(\Delta ABC\) suy ra \( EF // AC\) và \(EF = \dfrac{{AC}}{2}\) (1)
\(\Delta ADC\) có \(HA=HD\) và \(GD=GC\) nên \(HG\) là đường trung bình của \(\Delta ADC\) suy ra \( HG // AC\) và \(HG = \dfrac{{AC}}{2}\) (2)
Từ (1) và (2) suy ra \( EF//HG\) và \(EF = HG\)
Tứ giác \(EFGH\) có \( EF//HG\) và \(EF = HG\) nên là hình bình hành (dấu hiệu nhận biết hình bình hành).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 32 trang 116 Vở bài tập toán 8 tập 1 timdapan.com"







