Giải mục 3 trang 20, 21 SGK Toán 8 - Cùng khám phá
Cho hai đường thẳng
Hoạt động 4
Cho hai đường thẳng \(y = 2x - 1\) và \(y = x + 1\).
a) Hai đường thẳng này có song song với nhau không? Từ đó kết luận về số giao điểm của chúng
b) Vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ và tìm tọa độ giao điểm (nếu có).
Phương pháp giải:
Điều kiện của hai đường thẳng cắt nhau là \(a = a',b \ne b'\) và ngược lại. Sau đó vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ và tìm tọa độ giao điểm.
Lời giải chi tiết:
a) Hai đường thẳng này không song song với nhau vì hệ số góc không bằng nhau. Vì vậy hai đường thẳng này sẽ cắt nhau và chỉ có một giao điểm
b) Vẽ hệ trục tọa độ \(Oxy\).
Hàm số \(y = 2x - 1\)
Cho \(x = 0 = > y = - 1\)
Cho \(y = 0 = > x = \frac{1}{2}\)
Vậy đồ thị hàm số \(y = 2x - 1\) là đường thẳng đi qua hai điểm \(A\left( {0; - 1} \right),B\left( {\frac{1}{2};0} \right)\)
Hàm số \(y = x + 1\)
Cho \(x = 0 = > y = 1\)
Cho \(y = 0 = > x = - 1\)
Vậy đồ thị hàm số \(y = x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right),D\left( { - 1;0} \right)\)
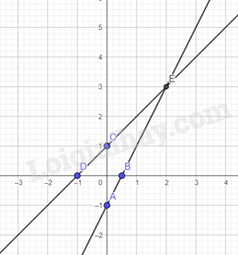
Giao điểm \(E\left( {2;3} \right)\).
Luyện tập 3
Cho hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\). Tìm giá trị của m và n để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau.
Phương pháp giải:
Dựa vào điều kiện của hai đường thẳng song song và hai đường thẳng cắt nhau để tìm giá trị của m và n.
Lời giải chi tiết:
a) Để hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\) là hai đường thẳng song song thì \(a = a',b \ne b'\) => \(m = 5,n \ne - 3\)
b) Để hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\) là hai đường thẳng cắt nhau thì \(a \ne a'\) => \(m \ne 5\).
Vận dụng 3
Một bè gỗ trôi theo dòng nước trên một khúc sông từ bến A đến bến B với tốc độ 4 km/h. Xuất phát cùng lúc với bè gỗ, một thuyền ngược dòng từ B về A với tốc độ 8 km/h. Hai bến sông A, B cách nhau 12 km.
a) Viết hàm số biểu thị quãng đường bè gỗ đi được sau x giờ
b) Viết hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ.
c) Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ. Từ đồ thị hãy cho biết sau bao lâu kể từ khi cùng xuất phát thì bè gỗ và thuyền gặp nhau.
Phương pháp giải:
Dựa vào mối quan hệ giữa quãng đường và tốc độ đề bài đưa ra viết hàm số biểu thị quãng đường bè gỗ đi được sau x giờ và hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ. Sau đó vẽ đồ thị của hai hàm số, áp dụng điều kiện đồ thị hai đường thẳng cắt nhau xác định giao điểm.
Lời giải chi tiết:
a) Hàm số biểu thị quãng đường bè gỗ đi được sau x giờ là: \(y = 4x\)
b) Hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ là: \(y = 12 - 8x\)
c) Vẽ hệ trục tọa độ \(Oxy\)
Hàm số \(y = 4x\) đi qua gốc tọa độ \(O\left( {0;0} \right)\)
Cho \(x - 1 = > y = 4\)
Vậy hàm số \(y = 4x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right),A\left( {1;4} \right)\)
Hàm số \(y = 12 - 8x\)
Cho \(x = 0 = > y = 12\)
Cho \(y = 0 = > x = \frac{3}{2}\)
Vậy hàm số \(y = 12 - 8x\) là đường thẳng đi qua hai điểm \(B\left( {0;12} \right),C\left( {\frac{3}{2};0} \right)\)

Từ đồ thị của hai hàm số trên ta thấy hai đường thẳng giao nhau tại \(A\left( {1;4} \right)\) có nghĩa là sau 1 giờ kể từ khi cùng xuất phát thì bè gỗ và thuyền gặp nhau.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 20, 21 SGK Toán 8 - Cùng khám phá timdapan.com"







