Giải mục 1 trang 17, 18, 19 SGK Toán 8 - Cùng khám phá
a) Vẽ đồ thị hai hàm số
Hoạt động 1
Hình 5.26 biểu diễn đồ thị của các hàm số bậc nhất \(y = 2x + 3,y = 2x\) và \(y = 2x - 4\). So sánh hệ số a của các hàm số trên. So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) .

Phương pháp giải:
Quan sát Hình 5.26 và các hàm số ta có thể xác định được các hệ số \(a\), sau đó so sánh hệ số \(a\) của các hàm số đó và so sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\).
Lời giải chi tiết:
Hàm số \(y = 2x + 3\) có \(a = 2\)
Hàm số \(y = 2x\) có \(a = 2\)
Hàm số \(y = 2x - 4\) có \(a = 2\)
Từ đó ta thấy các hệ số góc của ba hàm số này bằng nhau.
Các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) bằng nhau.
Hoạt động 2
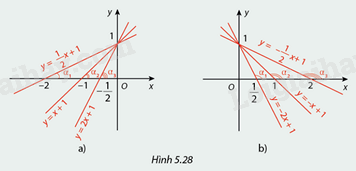
a) Hình 5.28a biểu diễn đồ thị của các hàm số bậc nhất với hệ số a > 0:
\(y = \frac{1}{2}x + 1\)
\(y = x + 1\)
\(y = 2x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
b) Hình 5.28b biểu diễn đồ thị của các hàm số bậc nhất với hệ số a < 0:
\(y = - 2x + 1\)
\(y = - x + 1\)
\(y = - \frac{1}{2}x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
Phương pháp giải:
Quan sát Hình 5.28 và các hàm số ta có thể xác định được các hệ số \(a\), sau đó so sánh hệ số \(a\) của các hàm số đó và so sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\).
Lời giải chi tiết:
a) Quan sát hình 5.28a ta thấy các góc \({\alpha _1} < {\alpha _2} < {\alpha _3}\)
Hàm số \(y = \frac{1}{2}x + 1\) có hệ số \({a_1} = \frac{1}{2}\)
Hàm số \(y = x + 1\) có hệ số \({a_2} = 1\)
Hàm số \(y = 2x + 1\) có hệ số \({a_3} = 2\)
Vậy qua đó ta được \(0 < {a_1} < {a_2} < {a_3}\)
b) Quan sát hình 5.28b ta thấy các góc \({\alpha _1} > {\alpha _2} > {\alpha _3}\)
Hàm số \(y = - 2x + 1\) có hệ số \({a_1} = - 2\)
Hàm số \(y = - x + 1\) có hệ số \({a_2} = - 1\)
Hàm số \(y = - \frac{1}{2}x + 1\) có hệ số \({a_3} = - \frac{1}{2}\)
Vậy qua đó ta được \({a_1} < {a_2} < {a_3} < 0\)
Luyện tập 1
Cho hàm số bậc nhất \(y = ax\) có đồ thị là đường thẳng d như Hình 5.29. Tìm hệ số góc a.

Phương pháp giải:
Hệ số \(a\) được gọi là hệ số góc của đường thẳng \(y = ax + b\) hay là hệ số góc của đồ thị hàm số \(y = ax + b\)\(\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Quan sát hình 5.29, ta thấy hàm số bậc nhất \(y = ax\) có hệ số góc \(a = \frac{y}{x} = \frac{3}{1} = 3\).
Vận dụng 1
Bạn Trọng tham gia cuộc thi trực tuyến “Tinh hoa Việt Nam” về những nét đặc sắc trong văn hóa nước ta. Khi mới tạo tài khoản dự thi, Trọng được tặng 50 điểm tích lũy. Mỗi khi trả lời đúng một câu hỏi, số điểm tích lũy T của Trọng được tăng theeo 5 điểm. Nếu trả lời sai câu hỏi thì không bị trừ điểm.
a) Tìm công thức biểu diễn hàm số T theo số câu hỏi n mà Trọng trả lời đúng
b) Tìm số điểm tích lũy của Trọng, biết rẳng Trọng đã trả lời đúng 18 câu hỏi.
Phương pháp giải:
Gọi số câu hỏi mà Trọng trả lời được là \(n\). Dựa vào các dữ liệu mà đề bài cho về mối quan hệ giữa các câu hỏi và điểm tích lũy, ta biểu diễn được hàm số T theo số câu hỏi \(n\) mà Trọng trả lời đúng, sau đó tìm số điểm tích lũy của Trọng khi trả lời được 18 câu hỏi.
Lời giải chi tiết:
a) Gọi số câu hỏi mà Trọng trả lời được là \(n\). Thì công thức biểu diễn hàm số T theo số câu hỏi \(n\) mà Trọng trả lời đúng là: \(T = 50 + 5n\)
b) Số điểm tích lũy của Trọng khi trả lời đúng 18 câu hỏi là: \(T = 50 + 5.8 = 90\) (điểm)
Vận dụng 2
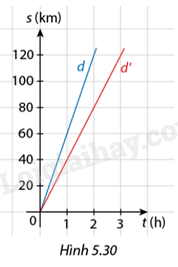
Trong Hình 5.30, các đường thẳng \(d\) và \(d'\) lần lượt chứa đồ thị quãng đường – thời gian của hai ô tô A và B chuyển động đều.
a) Tìm các số thích hợp cho ô trống trong Bảng 5.16.
b) Xác định hệ số góc của mỗi đường thẳng.
c) Tính tốc độ của mỗi xe. Em có nhận xét gì về tốc độ của mỗi xe và hệ số góc của đồ thị quãng đường – thời gian tương ứng?

Phương pháp giải:
Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ học ở bài trước để tìm các số thích hợp cho Bảng 5.16.
Xác định hệ số góc của mỗi đường thẳng bằng cách thay các giá trị \(x,y\) vừa tìm được vào công thức \(y = ax + b\). Sau đó tính tốc độ của mỗi xe dựa vào công thức \(s = v.t\).
Lời giải chi tiết:
a) Quan sát Hình 5.30 ta được Bảng 5.16 như sau: 
b) Quan sát Hình 5.30 ta thấy cả hai đường thẳng d và d’ đều đi qua gốc tọa độ \(O\left( {0;0} \right)\), vậy cả hai đường thẳng đều có dạng \(y = ax\).
Đường thẳng d đi qua điểm có tọa độ \(\left( {1;60} \right)\) thay vào hàm số \(y = ax\), ta có:
\(\begin{array}{l}60 = a.1\\ = > a = 60\end{array}\)
Vậy hệ số góc của đường thẳng d là \(a = 60\)
Đường thẳng d’ đi qua điểm có tọa độ \(\left( {1;40} \right)\) thay vào hàm số \(y = ax\), ta có:
\(\begin{array}{l}40 = a.1\\ = > a = 40\end{array}\)
Vậy hệ số góc của đường thẳng d’ là \(a = 40\)
c) Tốc độ của xe A là: \(v = \frac{s}{t} = \frac{{60}}{1} = 60\left( {km/h} \right)\)
Tốc độ của xe B là: \(v = \frac{s}{t} = \frac{{40}}{1} = 40\left( {km/h} \right)\)
Ta thấy tốc độ của mỗi xe bằng với hệ số góc của đồ thị quãng đường – thời gian tương ứng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 17, 18, 19 SGK Toán 8 - Cùng khám phá timdapan.com"







