Giải mục 2 trang 55, 56, 57, 58 Chuyên đề học tập Toán 10 - Chân trời sáng tạo
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
HĐ2
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
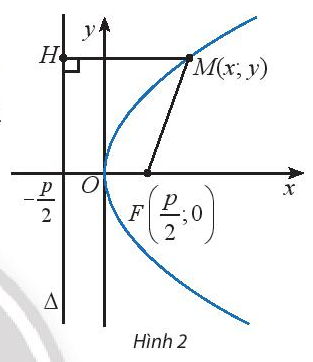
Lời giải chi tiết:
Tiêu điểm \(F(\frac{p}{2};0)\)
Ta có:
\(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + 2p{x_0}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\);
Thực hành 2
Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng.
a) Điểm \({M_1}(1; - 4)\) trên \(({P_1}):{y^2} = 16x\)
b) Điểm \({M_2}(3; - 3)\) trên \(({P_2}):{y^2} = 3x\)
c) Điểm \({M_3}(4;1)\) trên \(({P_3}):{y^2} = \frac{1}{4}x\)
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Với \(M({x_0};{y_0})\) thuộc parabol, bán kính qua tiêu: \(FM = {x_0} + \frac{p}{2}\)
Lời giải chi tiết:
a) \(({P_1}):{y^2} = 16x\)
Ta có \(2p = 16\), suy ra \(p = 8\). Vậy độ dài bán kính qua tiêu của điểm \({M_1}(1; - 4)\) là: \(FM = x + \frac{p}{2} = 1 + \frac{8}{2} = 5.\)
b) \(({P_2}):{y^2} = 3x\)
Ta có \(2p = 3\), suy ra \(p = \frac{3}{2}\). Vậy độ dài bán kính qua tiêu của điểm \({M_2}(3; - 3)\) là: \(FM = x + \frac{p}{2} = 3 + \frac{{\frac{3}{2}}}{2} = \frac{{15}}{4}.\)
c) \(({P_3}):{y^2} = \frac{1}{4}x\)
Ta có \(2p = \frac{1}{4}\), suy ra \(p = \frac{1}{8}\). Vậy độ dài bán kính qua tiêu của điểm \({M_3}(4;1)\) là: \(FM = x + \frac{p}{2} = 4 + \frac{{\frac{1}{8}}}{2} = \frac{{65}}{{16}}.\)
Vận dụng 2
Một cổng có dạng một đường parabol (P). Biết chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9m. Người ta muốn treo một ngôi sao tại tiêu điểm F của (P) bằng một đoạn dây nối từ đỉnh S của cổn. Tính khoảng cách từ tâm ngôi sao đến đỉnh cổng.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\)
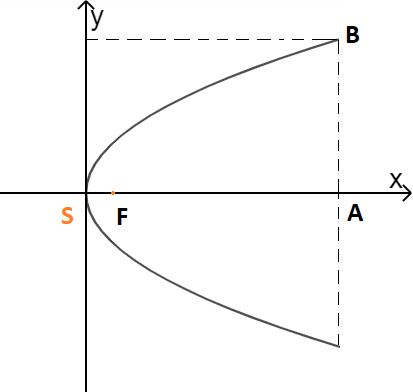
Chiều cao của cổng là 7,6 m nên \(A(7,6;0)\)
Khoản cách giữa hai chân cổng là 9m nên \(B(7,6;4,5)\)
\(B \in (P)\) suy ra \(4,{5^2} = 2p.7,6 \Rightarrow p = \frac{{405}}{{304}}\)
Tiêu điểm F của (P) có tọa độ: \(F\left( {\frac{{405}}{{608}};0} \right)\)
Hay khoảng cách từ tâm ngôi sao đến đỉnh cổng là \(\frac{{405}}{{608}} \approx 0,67(m)\),
Vận dụng 3
Mặt cắt của một chảo ăng-ten có dạng một parabol (P) có phương trình chính tắc \({y^2} = 0,25x\). Biết đầu thu tín hiệu của chảo ăng-ten tại tiêu điểm F của (P). Tính khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến F.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
(P) \({y^2} = 0,25x\) có \(2p = 0,25 \Leftrightarrow p = \frac{1}{8}\)
Khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến \(F\) là:
\(MF = {x_M} + \frac{p}{2} = 0,25 + \frac{{\frac{1}{8}}}{2} = 0,3125\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 55, 56, 57, 58 Chuyên đề học tập Toán 10 - Chân trời sáng tạo timdapan.com"







