Giải mục 2 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Cánh diều
Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:
Hoạt động 4
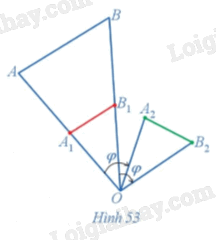
Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số \(\frac{1}{2}\);
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay \(\varphi = -60^\circ .\)
c) Nhận xét về mối liên hệ giữa độ dài các đoạn thẳng \(AB,{\rm{ }}{A_2}{B_2}.\)
Phương pháp giải:
Quan sát hình 53 để trả lời
Lời giải chi tiết:
a) Nối O với A và O với B, lấy điểm A1 là trung điểm của đoạn thẳng OA, lấy điểm B1 là trung điểm của đoạn thẳng OB. Khi đó \(\overrightarrow {O{A_1}} = \frac{1}{2}\overrightarrow {OA} ,\,\,\overrightarrow {O{B_1}} = \frac{1}{2}\overrightarrow {OB} \).
Do đó, A1, B1 tương ứng là ảnh của A, B qua phép vị tự tâm O tỉ số \(\frac{1}{2}\) nên đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số \(\frac{1}{2}\).
b) Phép quay với góc quay \(\varphi = -60^\circ \) có chiều quay cùng chiều kim đồng hồ.
Theo chiều quay cùng chiều kim đồng hồ, dựng góc \(\widehat {{A_1}O{A_2}} = 60^\circ \) sao cho \(O{A_1}\; = {\rm{ }}O{A_2}\); dựng góc \(\widehat {{B_1}O{B_2}} = 60^\circ \) sao cho \(O{B_1}\; = {\rm{ }}O{B_2}\). Khi đó ta có A2, B2 tương ứng là ảnh của A1, B1 qua phép quay tâm O với góc quay \(\varphi = -60^\circ \) nên đoạn thẳng \({A_2}{B_2}\) là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay \(\varphi = -60^\circ \).
c) Vì đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số \(\frac{1}{2}\) nên \({A_1}{B_1} = \frac{1}{2}AB\).
Vì đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép quay tâm O với góc quay \(\varphi = -60^\circ \) nên \({A_2}{B_2}\; = {\rm{ }}{A_1}{B_1}.\)
Từ đó suy ra \({A_2}{B_2}\; = \frac{1}{2}AB\)
Luyện tập 3
Người ta dùng một kính hiển vi có khả năng phóng to vật lên gấp 100 000 lần để quan sát một virus và đo được kích thước của virus là 2 mm. Hỏi kích thước thật của virus là bao nhiêu micromét (μm)?
Phương pháp giải:
Do qua kính hiển vi vật phóng to 100000 lần nên kích thước thật của virus giảm 100000 lần.
Lời giải chi tiết:
Kích thước thật của virus là
\(2{\rm{ }}:{\rm{ }}100{\rm{ }}000{\rm{ }} = {\rm{ }}0,00002{\rm{ }}\left( {mm} \right){\rm{ }} = {\rm{ }}0,02{\rm{ }}\left( {\mu m} \right).\)
Hoạt động 5
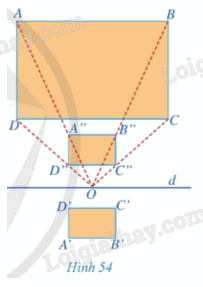
Quan sát Hình 54 và cho biết:
a) Hình chữ nhật A"B"C"D" nhận được từ hình chữ nhật ABCD bằng cách nào.
b) Hình chữ nhật A'B'C'D' nhận được từ hình chữ nhật A"B"C"D" bằng cách nào.
c) Phép đồng dạng nào biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
Phương pháp giải:
Quan sát hình 54 và sử dụng định lí Thales để trả lời
Lời giải chi tiết:
a) Áp dụng định lí Thales, ta có:
\(A''B''{\rm{ }}//{\rm{ }}AB\) nên \(\frac{{OA''}}{{OA}} = \frac{{OB''}}{{OB}}\)
\(B''C''{\rm{ }}//{\rm{ }}BC\) nên \(\frac{{OB''}}{{OB}} = \frac{{OC''}}{{OC}}\)
\(C''D''{\rm{ }}//{\rm{ }}CD\) nên \(\frac{{OC''}}{{OC}} = \frac{{OD''}}{{OD}}\)
\(D''A''{\rm{ }}//{\rm{ }}DA\) nên \(\frac{{OD''}}{{OD}} = \frac{{OA''}}{{OA}}\).
Từ đó suy ra \(\frac{{OA''}}{{OA}} = \frac{{OB''}}{{OB}} = \frac{{OC''}}{{OC}} = \frac{{OD''}}{{OD}} = k\) với k ≠ 0.
Do đó, \(\overrightarrow {OA''} = k\overrightarrow {OA} ,\,\,\overrightarrow {OB''} = k\overrightarrow {OB} ,\,\overrightarrow {OC''} = k\overrightarrow {OC} ,\,\overrightarrow {OD''} = k\overrightarrow {OD} \) nên ta có A", B", C", D" lần lượt là ảnh của A, B, C, D qua phép vị tự tâm O, tỉ số k. Như vậy, hình chữ nhật A"B"C"D" nhận được từ hình chữ nhật ABCD qua phép vị tự tâm O tỉ số k với \(k\; = \frac{{OA''}}{{OA}}\).
b) Qua phép đối xứng trục d, các điểm A", B", C", D" biến thành các điểm A', B', C', D'.
Do đó, hình chữ nhật A'B'C'D' nhận được từ hình chữ nhật A"B"C"D" qua phép đối xứng trục d.
c) Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k với \(k = \frac{{OA''}}{{OA}}\) và phép đối xứng trục d (\({V_{(O,{\rm{ }}k)}}\) trước, sau) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
Luyện tập 4
Trong Ví dụ 8, chứng minh rằng hai hình OMGE và COEN đồng dạng với nhau.
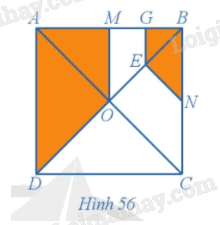
Phương pháp giải:
Quan sát hình 56 và dựa vào phép quay để làm
Lời giải chi tiết:

+) Vì O là giao hai đường chéo của hình vuông ABCD nên AC và BD vuông góc với nhau tại O và O là trung điểm của AC và BD, lại có AC = BD nên suy ra OA = OB = OC = OD.
Tam giác OBC cân tại O (OB = OC) có ON là đường trung tuyến nên ON là đường phân giác, suy ra \(\widehat {CON} = \widehat {BON} = \frac{{\widehat {BOC}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \).
Tương tự ta chứng minh được \(\widehat {BOM} = 45^\circ \) hay \(\widehat {EOM} = 45^\circ \).
Trên tia ON, lấy điểm C' sao cho OC' = OC. Trên tia OB, lấy điểm N' sao cho ON' = ON. Trên tia OM, lấy điểm E' sao cho OE' = OE.
Lại có \(\widehat {COC'} = \widehat {CON} = 45^\circ ;\,\widehat {NON'} = \widehat {BON} = 45^\circ ;\,\widehat {NON'} = \widehat {BON} = 45^\circ \)
Mà phép quay với góc quay 45° có chiều quay ngược chiều kim đồng hồ.
Do đó, ta có phép quay tâm O với góc quay 45° biến các điểm C, O, E, N tương ứng thành các điểm C'¸O, E', N' nên phép quay tâm O với góc quay 45° biến hình COEN thành hình C'OE'N' (1).
+) Giả sử hình vuông ABCD có cạnh là a
Khi đó \(BD = AC = \;a\sqrt 2 ;\,OB = OC = \frac{{a\sqrt 2 }}{2};\,ON = \;\frac{{AB}}{2} = \frac{a}{2}\)
Suy ra \(OE = \frac{{OB}}{2} = \frac{{a\sqrt 2 }}{4};\,OC' = OC = \;\frac{{a\sqrt 2 }}{2};\,ON' = ON = \;\frac{a}{2}\).
Suy ra \(\frac{{OE}}{{ON'}} = \frac{{\sqrt 2 }}{2},\,\frac{{ON}}{{OC'}} = \frac{{\sqrt 2 }}{2}\), do đó \(\frac{{OE}}{{ON'}} = \frac{{ON}}{{OC'}} = \frac{{\sqrt 2 }}{2}\).
Qua E, kẻ đường thẳng song song với E'N' cắt OM tại F, suy ra EF // E'N' nên theo định lí Thales trong tam giác OE'N' ta có \(\frac{{OF}}{{OE'}} = \frac{{OE}}{{ON'}} = \frac{{\sqrt 2 }}{2}\).
Từ đó suy ra \(\frac{{ON}}{{OC'}} = \frac{{OE}}{{ON'}} = \frac{{OF}}{{OE'}} = \frac{{\sqrt 2 }}{2}\) nên \(\overrightarrow {ON} = \frac{{\sqrt 2 }}{2}\overrightarrow {OC'} ;\,\overrightarrow {OE} = \frac{{\sqrt 2 }}{2}\overrightarrow {ON'} ;\,\overrightarrow {OF} = \frac{{\sqrt 2 }}{2}\overrightarrow {OE'} \).
Như vậy, ta có phép vị tự tâm O với tỉ số \(\frac{{\sqrt 2 }}{2}\) biến các điểm C'¸O, E', N' tương ứng thành các điểm N, O, F, E hay phép vị tự tâm O với tỉ số \(\frac{{\sqrt 2 }}{2}\)biến hình C'OE'N' thành hình NOFE (2).
+) Tam giác NOB vuông cân tại N có NE là đường trung tuyến nên NE cũng là đường cao và \(NE = \;\frac{{OB}}{2} = OE\), suy ra \(\widehat {NEO} = 90^\circ \) và EN = EO.
Tương tự, ta chứng minh được \(\widehat {MEO} = 90^\circ \) và EM = EO.
Ta chứng minh được EFMG là hình vuông nên \(\widehat {FEG} = 90^\circ \) và EF = EG.
Mà phép quay với góc quay \(-{\rm{ }}90^\circ \) có chiều quay cùng chiều kim đồng hồ.
Do đó, ta có phép quay tâm E với góc quay \(-{\rm{ }}90^\circ \) biến các điểm N, O, F, E tương ứng thành các điểm O, M, G, E hay phép quay tâm E với góc quay \(-{\rm{ }}90^\circ \) biến hình NOFE thành hình OMGE (3).
Từ (1), (2) và (3) suy ra hai hình OMGE và COEN đồng dạng với nhau.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Cánh diều timdapan.com"







