Giải mục 1 trang 93, 94, 95 SGK Toán 8 tập 2 - Kết nối tri thức

Hoạt động 1

Cho tam giác vuông ABC có hai cạnh góc vuông AB=3cm,AC=4cm (H.9.31). Hãy đo độ dài cạnh BC và so sánh hai đại lượng \(A{B^2} + A{C^2}\) với \(B{C^2}\)

Phương pháp giải:

Thay các giá trị AB=3cm, AC=4cm vào \(A{B^2} + A{C^2}\) với \(B{C^2}\)

Lời giải chi tiết:

- Đo độ dài có BC=5cm

- Có \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)

với \(B{C^2} = {5^2} = 25\)

=>\(A{B^2} + A{C^2} = B{C^2}\)

Hoạt động 2

Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32

- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c

- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?

- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao nhiêu?

- So sánh \({c^2} + 2{\rm{a}}b\) với \({\left( {a + b} \right)^2}\)để rút ra nhận xét về mối quan hệ giữa hai đại lượng \({c^2}\) và \({a^2} + {b^2}\).

Phương pháp giải:

- Tính diện tích tấm bìa của hình vuông.

- Tính diện tích phần bìa bị che lấp là hình vuông cạnh c.

Lời giải chi tiết:

Phần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là: \({c^2}\)

- Diện tích tấm bìa hình vuông là: \({\left( {a + b} \right)^2}\)

=> Diện tích bốn tam giác vuông là: \({\left( {a + b} \right)^2} - {c^2}\)

Câu hỏi

Tìm độ dài x, y trong hình 9.35

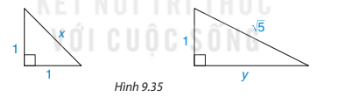
Phương pháp giải:

Áp dụng định lý Pythagore

Lời giải chi tiết:

Ta có: \({x^2} = {1^2} + {1^2} = 2 \Rightarrow x = \sqrt 2 \)

Ta có: \({\left( {\sqrt 5 } \right)^2} = {1^2} + {y^2} \Rightarrow {y^2} = {\left( {\sqrt 5 } \right)^2} - {1^2} = 5 - 1 = 4 \Rightarrow y = 2\)

Luyện tập 1

Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.

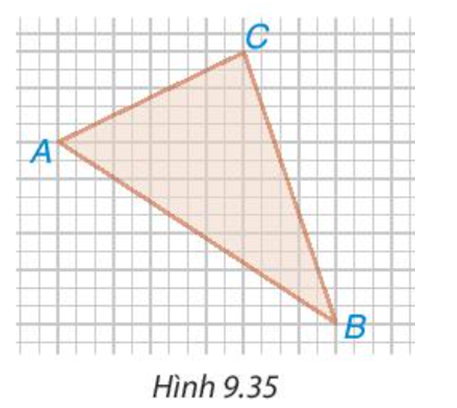
Phương pháp giải:

Áp dụng định lý Pythagore

Lời giải chi tiết:

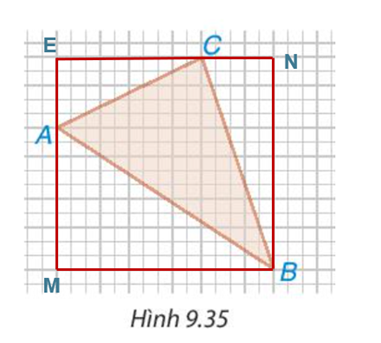
Từ A kẻ AM sao cho AM ⊥ MB

Tử C kẻ CM sao cho CN ⊥ NB

Từ C kẻ EC sao cho EC ⊥ EA

- Xét ΔAMB có AM ⊥ MB 

=> ΔAMB là tam giác vuông

=> \(A{B^2} = A{M^2} + M{B^2}\)

=> \(A{B^2} = {10^2} + {15^2}\)

=> \(AB = 5\sqrt {13} \) cm

- Xét ΔBNC có CN ⊥ NB

=> ΔBNC là tam giác vuông tại N

=> \(B{C^2} = N{B^2} + N{C^2}\)

=> \(BC = {15^2} + {5^2}\)

=> \(BC = 5\sqrt {10} \)cm

- Xét ΔAEC có EC ⊥ EA

=> ΔAEC là tam giác vuông tại E

=> \(A{C^2} = E{{\rm{A}}^2} + E{C^2}\)

=> \(A{C^2} = {5^2} + {10^2}\)

=> \(AC = 5\sqrt 5 \)cm

Vận dụng 1

Trở lại tình huống mở đầu. xem thành cầu thang như cạnh huyền BC của tam giác vuông ABC (hình 9.37). Tù đó, hãy tính độ dài cạnh BC để suy ra chiều dài cầu thang cần xây.

Phương pháp giải:

Áp dụng định lý Pythagore trong tam giác vuông ABC vuông tại A

Lời giải chi tiết:

Áp dụng định lý Pythagore trong tam giác vuông ABC vuông tại A ta có:

\(B{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = 5(m)\)

Vậy chiều dài của cầu thang là 5 m