Giải mục 1 trang 60, 61, 62 SGK Toán 10 tập 2 - Kết nối tri thức
Chọn chuyến đi (H.8.1) Chọn vé tàu (H.8.2) Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
HĐ1
Chọn chuyến đi (H.8.1)
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay.
Hỏi bạn An có bao nhiêu cách chọn?
Lời giải chi tiết:
Để đi bằng tàu hỏa bạn An có 7 cách chọn và đi bằng máy bay có 2 cách chọn.
Vậy bạn An có tất cả 7+2=9 cách chọn chuyến đi
HĐ2
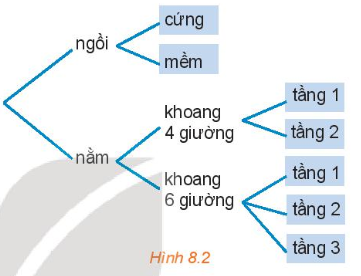
Chọn vé tàu (H.8.2)
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có 2 loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại không 4 giường và loại khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2, tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Lời giải chi tiết:
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2+3=5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2+5=7 (loại vé)
Luyện tập 1
Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
Phương pháp giải:
- không nguyên tố cùng nhau = có ước chung (khác 1).
- Mà 35 =5.7 nên ta tìm các số chia hết cho 5 hoặc 7.
Lời giải chi tiết:
Từ 1 đến 30 có:
- Có 6 số chia hết cho 5 là: 5, 10, 15, 20, 25, 30.
- Có 4 số chia hết cho 7 là: 7, 14, 21, 28.
Có tất cả 6+4= 10 số tự nhiên không nguyên tố cùng nhau với 35.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 60, 61, 62 SGK Toán 10 tập 2 - Kết nối tri thức timdapan.com"