Giải mục 1 trang 32, 33, 34 Chuyên đề học tập Toán 10 - Kết nối tri thức
Trong Bài 25 SGK Toán 10 (bộ sách Kết nối tri thức với cuộc sống), ta đã biết:
HĐ1
Trong Bài 25 SGK Toán 10 (bộ sách Kết nối tri thức với cuộc sống), ta đã biết:
\({(a + b)^1} = a + b\)
\({(a + b)^2} = {a^2} + 2ab + {b^2}\)
\({(a + b)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)
\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)
Với \(n \in \left\{ {1;2;3;4;5} \right\}\) trong khai triển của mỗi nhị thức \({(a + b)^n}\):
a) Có bao nhiêu số hạng?
b) Tổng số mũ của a và b trong mỗi số hạng bằng bao nhiêu?
c) Số mũ của a và b thay đổi thế nào khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sangg phải?
Lời giải chi tiết:
Trong khai triển của mỗi nhị thức \({(a + b)^n}\):
a) Có \(n + 1\) số hạng.
b) Tổng số mũ của a và b trong mỗi số hạng luôn bằng n.
c) Số mũ của a giảm dần từ n về 0 khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sangg phải.
Số mũ của b tăng dần từ 0 đến n khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sangg phải.
Câu hỏi
Tìm các hàng 7 và 8 của tam giác Pascal.
Lời giải chi tiết:
Ta đã có hàng 6 từ Hoạt động 2 trang 33:
\(\begin{array}{l}{(a + b)^6}\quad \quad 1\quad 6\quad 15\quad 20\quad 15\quad 6\quad 1\\{(a + b)^7}\quad \,1\quad 7\quad 21\quad 35\quad 35\quad 21\quad 7\quad 1\\{(a + b)^7}\;\;1\quad 8\quad 28\quad 56\quad 70\quad 56\quad 28\quad 8\quad 1\end{array}\)
Hàng 7: \(1 + 6 = 7,{\rm{ }}6 + 15 = 21,{\rm{ }}15 + 20 = 35\)
Hàng 8: \(1 + 7 = 8,{\rm{ 7}} + 21 = 28,{\rm{ 21 + 35 = 56,}}\;{\rm{35 + 35 = 70}}\)
Luyện tập 1
a) Sử dụng tam giác Pascal viết khai triển của \({(a + b)^7}\)
b) Sử dụng tam giác Pascal viết khai triển của \({(2x - 1)^4}\)
Phương pháp giải:
Dựa vào hàng tương ứng của tam giác Pascal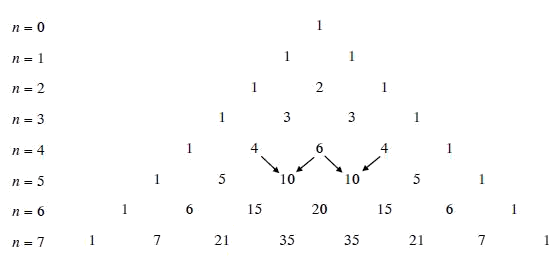
b) Viết khai triển của \({(a + b)^4}\)rồi thay \(a = 2x,b = - 1\) vào khai triển nhận được.
Lời giải chi tiết:
a) Khai triển của \({(a + b)^7}\) có dạng
\({(a + b)^7} = {a^7} + ?{a^6}b + ?{a^5}{b^2} + ?{a^4}{b^3} + ?{a^3}{b^4} + ?{a^2}{b^5} + ?a{b^6} + ?{b^7}\)
Các hệ số trong khai triển này là các hệ số ở hàng 7 của tam giác Pascal. Do đó ta có ngay
\({(a + b)^7} = {a^7} + 7{a^6}b + 21{a^5}{b^2} + 35{a^4}{b^3} + 35{a^3}{b^4} + 21{a^2}{b^5} + 7a{b^6} + {b^7}\)
b) Ta viết khai triển của \({(a + b)^4}\)rồi thay \(a = 2x,b = - 1\) vào khai triển nhận được.
Dựa vào hàng 4 của tam giác Pascal, ta có
\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)
Với \(a = 2x,b = - 1\) ta được:
\(\begin{array}{l}{(2x - 1)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}\left( { - 1} \right) + 6.{\left( {2x} \right)^2}{\left( { - 1} \right)^2} + 4.2x.{\left( { - 1} \right)^3} + {\left( { - 1} \right)^4}\\ = 16{x^4} - 32{x^3} + 24{x^2} - 8x + 1\end{array}\)
HĐ3
a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
\({(a + b)^1} = a + b = C_1^0a + C_1^1b\)
\({(a + b)^2} = {a^2} + 2ab + {b^2} = C_2^0{a^2} + C_2^1ab + C_2^2{b^2}\)
\({(a + b)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3} = C_3^0{a^3} + C_3^1{a^2}b + C_3^2a{b^2} + C_3^3{b^3}\)
\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4} = ...\)
\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5} = ...\)
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn \(C_4^1\) và \(C_4^3\), \(C_5^2\) và \(C_5^3\). Từ đó hãy dự đoán hệ thức giữa \(C_n^k\) và \(C_n^{n - k}(0 \le k \le n)\)
b) Từ tính chất của tam giác Pascal, hãy so sánh \(C_1^0 + C_1^1\) và \(C_2^1\), \(C_2^0 + C_2^1\) và \(C_3^1,...\) Từ đó hãy dự đoán hệ thức giữa \(C_{n - 1}^{k - 1} + C_{n - 1}^k\) và \(C_n^k.\)
Lời giải chi tiết:
a) \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4} = C_4^0{a^4} + C_4^1{a^3}b + C_4^2{a^2}{b^2} + C_4^3a{b^3} + C_4^4{b^4}\)
\(\begin{array}{l}{(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\\ = C_5^0{a^5} + C_5^1{a^4}b + C_5^2{a^3}{b^2} + C_5^3{a^2}{b^3} + C_5^4a{b^4} + C_5^5{b^5}\end{array}\)
Dễ thấy \(C_4^1 = C_4^3\) , \(C_5^2 = C_5^3\). Dự đoán \(C_n^k = C_n^{n - k}(0 \le k \le n)\)
b) Từ tính chất trong tam giác Pascal: Mọi số (khác 1) đều là tổng của hai số ở ngay phía trên nó.
Ta suy ra: \(C_1^0 + C_1^1 = C_2^1\), \(C_2^0 + C_2^1 = C_3^1\)
Dự đoán: \(C_{n - 1}^{k - 1} + C_{n - 1}^k = C_n^k.\)
Câu hỏi
Hãy chứng minh các công thức trên bằng cách sử dụng công thức tính số các tổ hợp

Phương pháp giải:
\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\)
Lời giải chi tiết:
Tính chất đối xứng
\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}} = \frac{{n!}}{{\left( {n - k} \right)!\left[ {n - (n - k)} \right]!}} = C_n^{n - k}\)
Hệ thức Pascal
\(\begin{array}{l}C_{n - 1}^{k - 1} + C_{n - 1}^k = \frac{{(n - 1)!}}{{(k - 1)!\left( {n - k} \right)!}} + \frac{{(n - 1)!}}{{k!\left( {n - 1 - k} \right)!}}\\ = \frac{{(n - 1)!}}{{(k - 1)!\left( {n - k - 1} \right)!}}\left( {\frac{1}{{n - k}} + \frac{1}{k}} \right)\\ = \frac{{(n - 1)!}}{{(k - 1)!\left( {n - k - 1} \right)!}}.\frac{n}{{(n - k).k}} = \frac{{n!}}{{k!\left( {n - k} \right)!}} = C_n^k\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 32, 33, 34 Chuyên đề học tập Toán 10 - Kết nối tri thức timdapan.com"







