Giải dự án 2 trang 112 SGK Toán 8 tập 1
Bác Hương có 250 triệu đồng muốn gửi tiết kiệm ở một ngân hàng và hai năm sau mới có nhu cầu sử dụng
Đề bài
Bác Hương có 250 triệu đồng muốn gửi tiết kiệm ở một ngân hàng và hai năm sau mới có nhu cầu sử dụng số tiền này. Dựa vào bảng lãi suất mà ngân hàng công bố tại thời điểm hiện tại, hãy tư vấn cho bác Hương phương án gửi tiết kiệm để số tiền lãi thu được sau hai năm gửi tiết kiệm là lớn nhất.
Ở đây, giả sử các lãi suất đã công bố là không thay đổi trong suốt quá trình bác Hương gửi tiết kiệm.
Phương pháp giải - Xem chi tiết
Dựa vào bảng lãi suất các kì hạn của một ngân hàng.
Sử dụng công thức lãi kép để tính số tiền nhận được sau hai năm theo mỗi kì hạn gửi. Từ đó lựa chọn được kì hạn gửi tối ưu.
Lời giải chi tiết
Bảng lãi suất hàng năm theo kì hạn của một số tháng của ngân hàng TMCP Sài Gòn (SCB) công bố tại thời điểm 21/08/2023 như sau:
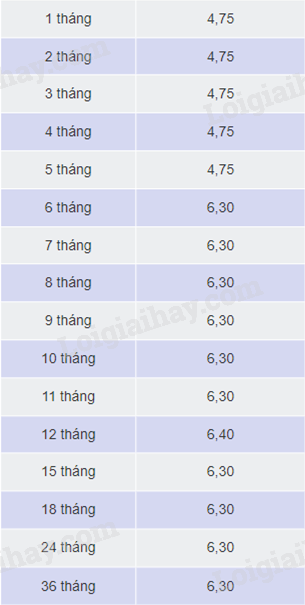
Để tính số tiền nhận được cả gốc lẫn lãi sau mà bác Hương nhận được khi gửi tiết kiệm một khoản tiền gốc P = 250 (triệu đồng) với lãi suất hàng năm r, được tính lãi n lần trong 1 năm, sau N kì gửi là \(P.{\left( {1 + \frac{r}{n}} \right)^N}\)
|
Kì hạn |
Lãi suất |
Số tiền nhận được sau 2 năm (triệu đồng) |
|
1 tháng |
4,75% |
\(250.{\left( {1 + \frac{{4,75\% }}{{12}}} \right)^{24}} \approx 274,863\) |
|
2 tháng |
4,75% |
\(250.{\left( {1 + \frac{{4,75\% }}{6}} \right)^{12}} \approx 274,811\) |
|
3 tháng |
4,75% |
\(250.{\left( {1 + \frac{{4,75\% }}{4}} \right)^8} \approx 274,861\) |
|
4 tháng |
4,75% |
\(250.{\left( {1 + \frac{{4,75\% }}{3}} \right)^6} \approx 274,71\) |
|
6 tháng |
6,3% |
\(250.{\left( {1 + \frac{{6,3\% }}{2}} \right)^4} \approx 283,02\) |
|
12 tháng |
6,4% |
\(250.{\left( {1 + \frac{{6,4\% }}{1}} \right)^2} \approx 283,024\) |
Do đó, theo lãi suất kì hạn một số tháng ở trên, bác Hương nên gửi kì hạn là 12 tháng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải dự án 2 trang 112 SGK Toán 8 tập 1 timdapan.com"







